dijkstra algo added

dsa/Algorithms/_category_.json

@@ -0,0 +1,8 @@
+{
+    "label": "Algorithms",
+    "position": 7,
+    "link": {
+      "type": "generated-index",
+      "description": "In This section all the Algorithms are defined in DSA for graphs,trees,DP are meant to be added"
+    }
+  }

dsa/Algorithms/dijkstra.md

@@ -0,0 +1,365 @@
+---
+id: dijkstra
+title: Dijkstra's Algorithm 
+sidebar_label: Dijkstra's Algorithm 
+tags: [python, java, c++, javascript, programming, algorithms, dijkstra, graph, shortest-path, data structures, tutorial, in-depth]
+description: In this tutorial, we will learn about Dijkstra's Algorithm and its implementation in Python, Java, C++, and JavaScript with detailed explanations and examples.
+---
+
+# Dijkstra's Algorithm 
+
+Dijkstra's Algorithm is a popular algorithm used for finding the shortest paths between nodes in a graph. This tutorial will cover the basics of Dijkstra's Algorithm, its applications, and how to implement it in Python, Java, C++, and JavaScript. We will also delve into various optimizations and advanced use cases.
+
+## Introduction to Dijkstra's Algorithm
+
+Dijkstra's Algorithm was conceived by computer scientist Edsger W. Dijkstra in 1956. It is used to find the shortest path from a starting node to all other nodes in a weighted graph, where the weights represent the cost to traverse from one node to another.
+
+## How Dijkstra's Algorithm Works
+
+- **Initialization**: Start with a set of nodes. Assign a tentative distance value to every node: set it to zero for the initial node and to infinity for all other nodes. Set the initial node as the current node.
+- **Visit Neighbors**: For the current node, consider all its unvisited neighbors and calculate their tentative distances. Compare the newly calculated tentative distance to the current assigned value and assign the smaller one.
+- **Mark Visited**: Once all neighbors are visited, mark the current node as visited. A visited node will not be checked again.
+- **Select Next Node**: Select the unvisited node that is marked with the smallest tentative distance and set it as the new current node.
+- **Repeat**: Continue the process until all nodes have been visited.
+
+![image](https://cdn.hashnode.com/res/hashnode/image/upload/v1671745151505/5488136c-81a8-4a65-9d52-fa966d645b3f.png)
+
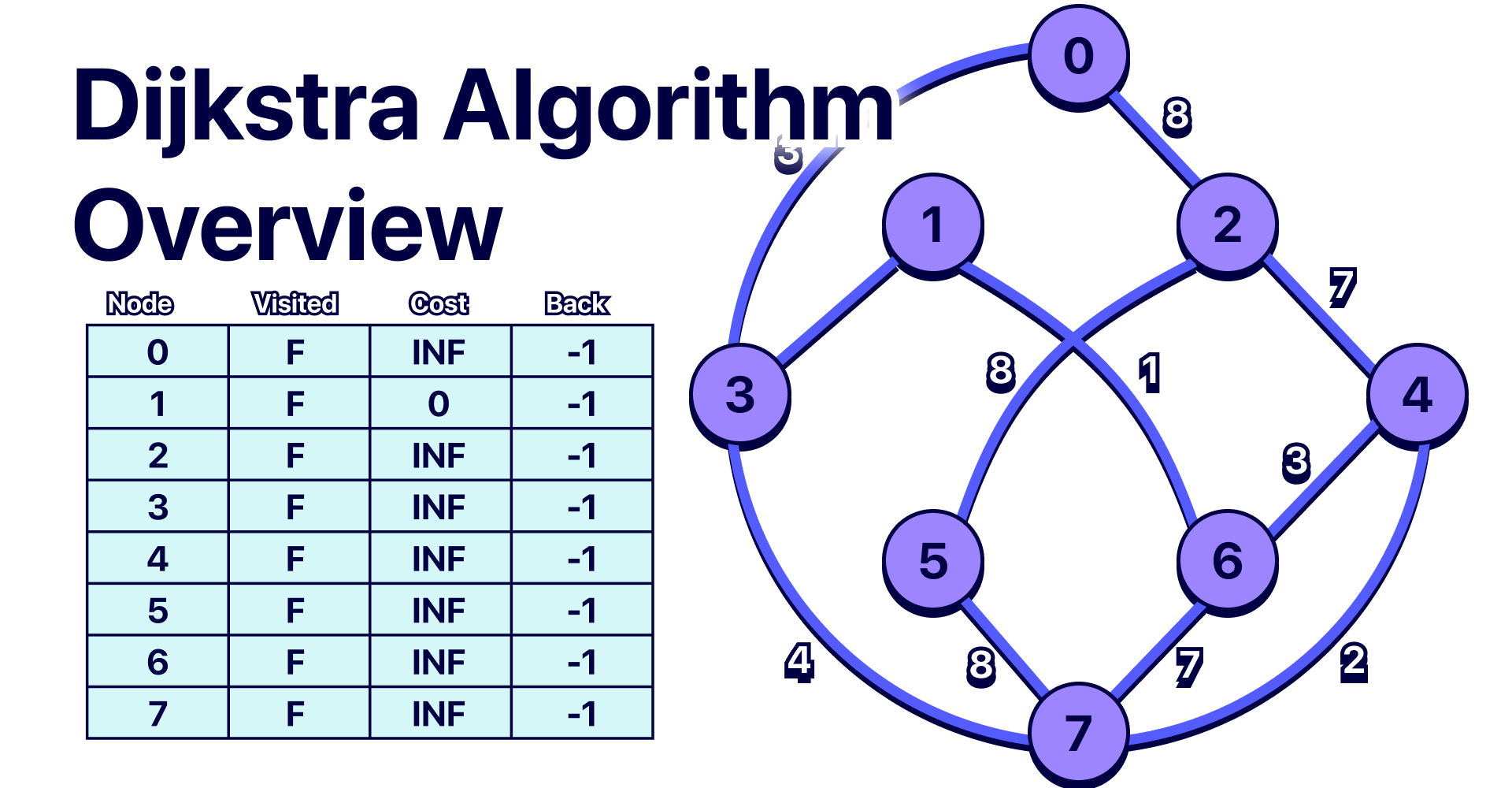+## Pseudocode for Dijkstra's Algorithm
+
+Here is the pseudocode for Dijkstra's Algorithm:
+
+```
+function Dijkstra(Graph, source):
+    create vertex set Q
+
+    for each vertex v in Graph:          
+        dist[v] ← INFINITY                 
+        prev[v] ← UNDEFINED                
+        add v to Q                         
+    dist[source] ← 0                       
+
+    while Q is not empty:
+        u ← vertex in Q with min dist[u]    
+        remove u from Q 
+
+        for each neighbor v of u:           
+            alt ← dist[u] + length(u, v)
+            if alt < dist[v]:              
+                dist[v] ← alt
+                prev[v] ← u
+
+    return dist[], prev[]
+```
+
+## Implementing Dijkstra's Algorithm
+
+### Python Implementation
+
+```python
+import heapq
+
+def dijkstra(graph, start):
+    priority_queue = [(0, start)]
+    distances = {vertex: float('infinity') for vertex in graph}
+    distances[start] = 0
+    previous_nodes = {vertex: None for vertex in graph}
+
+    while priority_queue:
+        current_distance, current_vertex = heapq.heappop(priority_queue)
+
+        if current_distance > distances[current_vertex]:
+            continue
+
+        for neighbor, weight in graph[current_vertex].items():
+            distance = current_distance + weight
+
+            if distance < distances[neighbor]:
+                distances[neighbor] = distance
+                previous_nodes[neighbor] = current_vertex
+                heapq.heappush(priority_queue, (distance, neighbor))
+
+    return distances, previous_nodes
+
+def shortest_path(graph, start, goal):
+    distances, previous_nodes = dijkstra(graph, start)
+    path = []
+    while goal:
+        path.append(goal)
+        goal = previous_nodes[goal]
+    return path[::-1]
+
+graph = {
+    'A': {'B': 1, 'C': 4},
+    'B': {'A': 1, 'C': 2, 'D': 5},
+    'C': {'A': 4, 'B': 2, 'D': 1},
+    'D': {'B': 5, 'C': 1}
+}
+
+print(shortest_path(graph, 'A', 'D'))
+```
+
+### Java Implementation
+
+```java
+import java.util.*;
+
+public class Dijkstra {
+
+    public static void dijkstra(Map<String, Map<String, Integer>> graph, String start) {
+        PriorityQueue<Node> priorityQueue = new PriorityQueue<>(Comparator.comparingInt(node -> node.distance));
+        Map<String, Integer> distances = new HashMap<>();
+        Map<String, String> previousNodes = new HashMap<>();
+
+        for (String vertex : graph.keySet()) {
+            distances.put(vertex, Integer.MAX_VALUE);
+            previousNodes.put(vertex, null);
+        }
+        distances.put(start, 0);
+        priorityQueue.add(new Node(start, 0));
+
+        while (!priorityQueue.isEmpty()) {
+            Node current = priorityQueue.poll();
+
+            if (current.distance > distances.get(current.name)) {
+                continue;
+            }
+
+            for (Map.Entry<String, Integer> neighbor : graph.get(current.name).entrySet()) {
+                int distance = current.distance + neighbor.getValue();
+
+                if (distance < distances.get(neighbor.getKey())) {
+                    distances.put(neighbor.getKey(), distance);
+                    previousNodes.put(neighbor.getKey(), current.name);
+                    priorityQueue.add(new Node(neighbor.getKey(), distance));
+                }
+            }
+        }
+
+        for (Map.Entry<String, Integer> entry : distances.entrySet()) {
+            System.out.println(entry.getKey() + " : " + entry.getValue());
+        }
+    }
+
+    public static List<String> shortestPath(Map<String, Map<String, Integer>> graph, String start, String goal) {
+        dijkstra(graph, start);
+        List<String> path = new ArrayList<>();
+        for (String at = goal; at != null; at = previousNodes.get(at)) {
+            path.add(at);
+        }
+        Collections.reverse(path);
+        return path;
+    }
+
+    public static void main(String[] args) {
+        Map<String, Map<String, Integer>> graph = new HashMap<>();
+        graph.put("A", Map.of("B", 1, "C", 4));
+        graph.put("B", Map.of("A", 1, "C", 2, "D", 5));
+        graph.put("C", Map.of("A", 4, "B", 2, "D", 1));
+        graph.put("D", Map.of("B", 5, "C", 1));
+
+        System.out.println(shortestPath(graph, "A", "D"));
+    }
+
+    static class Node {
+        String name;
+        int distance;
+
+        Node(String name, int distance) {
+            this.name = name;
+            this.distance = distance;
+        }
+    }
+}
+```
+
+### C++ Implementation
+
+```cpp
+#include <iostream>
+#include <vector>
+#include <unordered_map>
+#include <queue>
+#include <stack>
+#include <limits>
+#include <algorithm>
+
+using namespace std;
+
+typedef pair<int, int> Node;
+typedef unordered_map<string, unordered_map<string, int>> Graph;
+
+unordered_map<string, int> dijkstra(const Graph& graph, const string& start, unordered_map<string, string>& previousNodes) {
+    unordered_map<string, int> distances;
+    for (const auto& node : graph) {
+        distances[node.first] = numeric_limits<int>::max();
+    }
+    distances[start] = 0;
+
+    auto cmp = [](Node left, Node right) { return left.second > right.second; };
+    priority_queue<Node, vector<Node>, decltype(cmp)> priorityQueue(cmp);
+    priorityQueue.push({start, 0});
+
+    while (!priorityQueue.empty()) {
+        string current = priorityQueue.top().first;
+        int currentDistance = priorityQueue.top().second;
+        priorityQueue.pop();
+
+        if (currentDistance > distances[current]) {
+            continue;
+        }
+
+        for (const auto& neighbor : graph.at(current)) {
+            int distance = currentDistance + neighbor.second;
+            if (distance < distances[neighbor.first]) {
+                distances[neighbor.first] = distance;
+                previousNodes[neighbor.first] = current;
+                priorityQueue.push({neighbor.first, distance});
+            }
+        }
+    }
+
+    return distances;
+}
+
+vector<string> shortestPath(const Graph& graph, const string& start, const string& goal) {
+    unordered_map<string, string> previousNodes;
+    dijkstra(graph, start, previousNodes);
+
+    vector<string> path;
+    for (string at = goal; !at.empty(); at = previousNodes[at]) {
+        path.push_back(at);
+    }
+    reverse(path.begin(), path.end());
+    return path;
+}
+
+int main() {
+    Graph graph = {
+        {"A", {{"B", 1}, {"C", 4}}},
+        {"B", {{"A", 1}, {"C", 2}, {"D", 5}}},
+        {"C", {{"A", 4}, {"B", 2}, {"D", 1}}},
+        {"D", {{"B", 5}, {"C", 1}}}
+    };
+
+    vector<string> path = shortestPath(graph, "A", "D");
+    for (const string& node : path) {
+        cout << node << " ";
+    }
+    cout << endl;
+    return 0;
+}
+```
+
+### JavaScript Implementation
+
+```javascript
+function dijkstra(graph, start) {
+    let distances = {};
+    let previousNodes = {};
+    let priorityQueue = new PriorityQueue();
+
+    for (let vertex in graph) {
+        if (vertex === start) {
+            distances[vertex] = 0;
+            priorityQueue.enqueue(vertex, 0);
+        } else {
+
+
+ distances[vertex] = Infinity;
+            priorityQueue.enqueue(vertex, Infinity);
+        }
+        previousNodes[vertex] = null;
+    }
+
+    while (!priorityQueue.isEmpty()) {
+        let currentVertex = priorityQueue.dequeue().element;
+
+        for (let neighbor in graph[currentVertex]) {
+            let distance = distances[currentVertex] + graph[currentVertex][neighbor];
+            if (distance < distances[neighbor]) {
+                distances[neighbor] = distance;
+                previousNodes[neighbor] = currentVertex;
+                priorityQueue.enqueue(neighbor, distance);
+            }
+        }
+    }
+
+    return { distances, previousNodes };
+}
+
+function shortestPath(graph, start, goal) {
+    let { distances, previousNodes } = dijkstra(graph, start);
+    let path = [];
+    while (goal) {
+        path.push(goal);
+        goal = previousNodes[goal];
+    }
+    return path.reverse();
+}
+
+class PriorityQueue {
+    constructor() {
+        this.values = [];
+    }
+
+    enqueue(element, priority) {
+        this.values.push({ element, priority });
+        this.sort();
+    }
+
+    dequeue() {
+        return this.values.shift();
+    }
+
+    isEmpty() {
+        return this.values.length === 0;
+    }
+
+    sort() {
+        this.values.sort((a, b) => a.priority - b.priority);
+    }
+}
+
+let graph = {
+    'A': { 'B': 1, 'C': 4 },
+    'B': { 'A': 1, 'C': 2, 'D': 5 },
+    'C': { 'A': 4, 'B': 2, 'D': 1 },
+    'D': { 'B': 5, 'C': 1 }
+};
+
+console.log(shortestPath(graph, 'A', 'D'));
+```
+
+## Applications of Dijkstra's Algorithm
+
+- **Network Routing**: Finding the shortest path in network routing protocols such as OSPF.
+- **Map Services**: Computing the shortest routes in map services like Google Maps.
+- **Robotics**: Pathfinding in autonomous robots to navigate through environments.
+- **Game Development**: Pathfinding for game AI to navigate through game worlds.
+
+## Advanced Topics and Optimizations
+
+### Bidirectional Dijkstra
+
+Bidirectional Dijkstra runs two simultaneous searches: one forward from the source and one backward from the target. This can significantly speed up the search in large graphs.
+
+### Time Complexity
+
+The time complexity of Dijkstra's Algorithm depends on the data structures used:
+- Using a simple list: O(V^2)
+- Using a binary heap (priority queue): O((V + E) log V)
+- Using a Fibonacci heap: O(V log V + E)
+
+### Handling Negative Weights
+
+Dijkstra's Algorithm does not work with graphs that have negative weights. For such graphs, the Bellman-Ford Algorithm or Johnson's Algorithm can be used.
+
+### Path Reconstruction
+
+To reconstruct the shortest path from the source to a target node, we can backtrack from the target node using the `previous_nodes` dictionary.
+
+## Conclusion
+
+In this tutorial, we covered the fundamentals of Dijkstra's Algorithm, its implementation in Python, Java, C++, and JavaScript, and various optimizations and applications. Dijkstra's Algorithm is a powerful tool for finding the shortest path in graphs and is widely used in numerous domains. By mastering this algorithm, you can effectively solve a variety of shortest path problems in your projects.
+
+Happy coding!