From 2e2dd5033f7af688b7f5629e25f1d325ab7b0597 Mon Sep 17 00:00:00 2001
From: Hitesh4278 <97452642+Hitesh4278@users.noreply.github.com>
Date: Fri, 14 Jun 2024 11:19:29 +0000
Subject: [PATCH 1/4] Added the Solution for Frequency of the Most Frequent
Element
---
dsa-problems/leetcode-problems/1800-1899.md | 2 +-
...-frequency-of-the-most-frequent-element.md | 255 ++++++++++++++++++
2 files changed, 256 insertions(+), 1 deletion(-)
create mode 100644 dsa-solutions/lc-solutions/1800-1899/1838-frequency-of-the-most-frequent-element.md
diff --git a/dsa-problems/leetcode-problems/1800-1899.md b/dsa-problems/leetcode-problems/1800-1899.md
index 6fbb45b63..571c352a7 100644
--- a/dsa-problems/leetcode-problems/1800-1899.md
+++ b/dsa-problems/leetcode-problems/1800-1899.md
@@ -242,7 +242,7 @@ export const problems = [
"problemName": "1838. Frequency of the Most Frequent Element",
"difficulty": "Medium",
"leetCodeLink": "https://leetcode.com/problems/frequency-of-the-most-frequent-element",
- "solutionLink": "#"
+ "solutionLink": "/dsa-solutions/lc-solutions/1800-1899/frequency-of-the-most-frequent-element"
},
{
"problemName": "1839. Longest Substring Of All Vowels in Order",
diff --git a/dsa-solutions/lc-solutions/1800-1899/1838-frequency-of-the-most-frequent-element.md b/dsa-solutions/lc-solutions/1800-1899/1838-frequency-of-the-most-frequent-element.md
new file mode 100644
index 000000000..eddf02212
--- /dev/null
+++ b/dsa-solutions/lc-solutions/1800-1899/1838-frequency-of-the-most-frequent-element.md
@@ -0,0 +1,255 @@
+---
+id: frequency-of-the-most-frequent-element
+title: Frequency of the Most Frequent Element
+sidebar_label: 1838 -Frequency of the Most Frequent Element
+tags:
+- Array
+- Binary Search
+- Greedy
+- Sliding Window
+- Sorting
+- Prefix Sum
+
+description: "This is a solution to the Frequency of the Most Frequent Element problem on LeetCode."
+---
+
+## Problem Description
+The frequency of an element is the number of times it occurs in an array.
+
+You are given an integer array nums and an integer k. In one operation, you can choose an index of nums and increment the element at that index by 1.
+
+Return the maximum possible frequency of an element after performing at most k operations.
+
+### Examples
+
+**Example 1:**
+
+```
+Input: nums = [1,2,4], k = 5
+Output: 3
+Explanation: Increment the first element three times and the second element two times to make nums = [4,4,4].
+4 has a frequency of 3.
+
+```
+
+**Example 2:**
+```
+Input: nums = [1,4,8,13], k = 5
+Output: 2
+Explanation: There are multiple optimal solutions:
+- Increment the first element three times to make nums = [4,4,8,13]. 4 has a frequency of 2.
+- Increment the second element four times to make nums = [1,8,8,13]. 8 has a frequency of 2.
+- Increment the third element five times to make nums = [1,4,13,13]. 13 has a frequency of 2.
+```
+
+**Example 3:**
+```
+Input: nums = [3,9,6], k = 2
+Output: 1
+```
+
+### Constraints
+
+- `1 <= nums.length <= 10^5`
+- `1 <= nums[i] <= 10^5`
+- `1 <= k <= 10^5`
+## Solution for Frequency of the Most Frequent Element Problem
+### Approach
+To determine the amount needed to convert the current sliding window [1, 2, 4] into [4, 4, 4], we use the formula (num_right×(right−left+1))−total, where num_right is the value we want to fill the window with (in this case, 4), right and left are the indices defining the window, and total is the sum of the current window. If this amount is within the budget k, i.e., (num_right×(right−left+1))−total≤k, then it is possible to achieve the desired frequency with a cost equal to the window length (right - left + 1).
+
+#### Steps
+##### Sorting:
+- Sorting the array helps to bring similar values closer together. This makes it easier to increase the frequency of a number by making other numbers in the subarray equal to it with minimal increments.
+##### Sliding Window:
+
+- The sliding window technique allows us to consider subarrays of the sorted array incrementally.
+- We maintain a window [i, j] where j is the current end of the window, and i is the start.
+##### Sum Calculation:
+- We keep a running sum of the elements within the window.
+- For each new element added to the window (i.e., extending j), we calculate the total number of operations needed to make all elements in the window equal to the current element nums[j].
+- This is checked using the formula (j−i+1)×nums[j]−sum. If this value is greater than k, it means we need more than k operations to make all elements equal to nums[j].
+##### Adjusting the Window:
+
+- If the current window requires more than k operations, we shrink the window from the left by incrementing i until the condition is satisfied.
+- If the condition is satisfied, it means the current window can be made equal with at most k increments, and we update the maximum frequency (maxFreq) with the size of the current window.
+##### Result:
+- The maximum frequency (maxFreq) found during the iterations will be the result.
+
+
+
+
+
+ #### Implementation
+ ```jsx live
+ function Solution(arr) {
+ function maxFrequency(nums, k) {
+ nums.sort((a, b) => a - b);
+ let maxFreq = 1;
+ let i = 0;
+ let sum = 0;
+
+ for (let j = 0; j < nums.length; j++) {
+ sum += nums[j];
+ while ((j - i + 1) * nums[j] - sum > k) {
+ sum -= nums[i];
+ i++;
+ }
+ maxFreq = Math.max(maxFreq, j - i + 1);
+ }
+
+ return maxFreq;
+ }
+ const input = [1, 2 ,4];
+ const k = 5
+ const output = maxFrequency(input , k) ;
+ return (
+
+
+ Input:
+ {JSON.stringify(input)}
+
+
+ Output: {output.toString()}
+
+
+ );
+ }
+ ```
+
+ #### Complexity Analysis
+
+ - Time Complexity: $ O(nlogn) $ because of sorting, where n is the size of array
+ - Space Complexity: $ O(1) $
+
+ ## Code in Different Languages
+
+
+
+ ```javascript
+ function maxFrequency(nums, k) {
+ nums.sort((a, b) => a - b);
+ let maxFreq = 1;
+ let i = 0;
+ let sum = 0;
+
+ for (let j = 0; j < nums.length; j++) {
+ sum += nums[j];
+ while ((j - i + 1) * nums[j] - sum > k) {
+ sum -= nums[i];
+ i++;
+ }
+ maxFreq = Math.max(maxFreq, j - i + 1);
+ }
+
+ return maxFreq;
+}
+ ```
+
+
+
+
+ ```typescript
+ function maxFrequency(nums: number[], k: number): number {
+ nums.sort((a, b) => a - b);
+ let maxFreq = 1;
+ let i = 0;
+ let sum = 0;
+
+ for (let j = 0; j < nums.length; j++) {
+ sum += nums[j];
+ while ((j - i + 1) * nums[j] - sum > k) {
+ sum -= nums[i];
+ i++;
+ }
+ maxFreq = Math.max(maxFreq, j - i + 1);
+ }
+
+ return maxFreq;
+}
+
+ ```
+
+
+
+ ```python
+ class Solution:
+ def maxFrequency(self, nums, k):
+ nums.sort()
+ maxFreq = 1
+ i = 0
+ sum = 0
+
+ for j in range(len(nums)):
+ sum += nums[j]
+ while (j - i + 1) * nums[j] - sum > k:
+ sum -= nums[i]
+ i += 1
+ maxFreq = max(maxFreq, j - i + 1)
+
+ return maxFreq
+
+ ```
+
+
+
+
+ ```java
+ import java.util.Arrays;
+
+public class Solution {
+ public int maxFrequency(int[] nums, int k) {
+ Arrays.sort(nums);
+ long maxFreq = 1;
+ long i = 0;
+ long sum = 0;
+
+ for (long j = 0; j < nums.length; j++) {
+ sum += nums[(int) j];
+ while ((j - i + 1) * nums[(int) j] - sum > k) {
+ sum -= nums[(int) i];
+ i++;
+ }
+ maxFreq = Math.max(maxFreq, j - i + 1);
+ }
+
+ return (int) maxFreq;
+ }
+}
+
+ ```
+
+
+
+
+ ```cpp
+ class Solution {
+public:
+ int maxFrequency(vector& nums, int k) {
+ sort(nums.begin(), nums.end());
+ long maxFreq = 1;
+ long i = 0;
+ long j = 0;
+ long long sum = 0;
+
+ while (j < nums.size()) {
+ sum += nums[j];
+ while ((j - i + 1) * nums[j] - sum > k) sum -= nums[i++];
+ maxFreq =max(maxFreq, j-i+1);
+ j++;
+ }
+ return maxFreq;
+ }
+};
+ ```
+
+
+
+
+
+
+## References
+
+- **LeetCode Problem**: [Frequency of the Most Frequent Element](https://leetcode.com/problems/frequency-of-the-most-frequent-element/description/)
+
+- **Solution Link**: [LeetCode Solution](https://leetcode.com/problems/frequency-of-the-most-frequent-element/solution)
+
From a81f30d2cf7b79c5f0d35bb46186f30613a8b35e Mon Sep 17 00:00:00 2001
From: Hitesh4278 <97452642+Hitesh4278@users.noreply.github.com>
Date: Fri, 14 Jun 2024 12:11:47 +0000
Subject: [PATCH 2/4] Added the solution of Path With Minimum Effort
---
dsa-problems/leetcode-problems/1600-1699.md | 2 +-
.../1631-path-with-minimum-effort.md | 352 ++++++++++++++++++
2 files changed, 353 insertions(+), 1 deletion(-)
create mode 100644 dsa-solutions/lc-solutions/1600-1699/1631-path-with-minimum-effort.md
diff --git a/dsa-problems/leetcode-problems/1600-1699.md b/dsa-problems/leetcode-problems/1600-1699.md
index fd9521dab..74937d1b5 100644
--- a/dsa-problems/leetcode-problems/1600-1699.md
+++ b/dsa-problems/leetcode-problems/1600-1699.md
@@ -200,7 +200,7 @@ export const problems = [
"problemName": "1631. Path With Minimum Effort",
"difficulty": "Medium",
"leetCodeLink": "https://leetcode.com/problems/path-with-minimum-effort",
- "solutionLink": "#"
+ "solutionLink": "/dsa-solutions/lc-solutions/1600-1631/path-with-minimum-effort"
},
{
"problemName": "1632. Rank Transform of a Matrix",
diff --git a/dsa-solutions/lc-solutions/1600-1699/1631-path-with-minimum-effort.md b/dsa-solutions/lc-solutions/1600-1699/1631-path-with-minimum-effort.md
new file mode 100644
index 000000000..9a79ccd98
--- /dev/null
+++ b/dsa-solutions/lc-solutions/1600-1699/1631-path-with-minimum-effort.md
@@ -0,0 +1,352 @@
+---
+id: path-with-minimum-effort
+title: Path With Minimum Effort
+sidebar_label: 1631 - Path With Minimum Effort
+tags:
+- Array
+- Binary Search
+- Depth-First Search
+- Breadth-First Search
+- Union Find
+- Heap (Priority Queue)
+- Matrix
+
+description: "This is a solution to the Path With Minimum Effort problem on LeetCode."
+---
+
+## Problem Description
+You are a hiker preparing for an upcoming hike. You are given heights, a 2D array of size rows x columns, where `heights[row][col]` represents the height of cell (row, col). You are situated in the top-left cell, `(0, 0)`, and you hope to travel to the bottom-right cell, `(rows-1, columns-1) (i.e., 0-indexed)`. You can move up, down, left, or right, and you wish to find a route that requires the minimum effort.
+
+A route's effort is the maximum absolute difference in heights between two consecutive cells of the route.
+
+Return the minimum effort required to travel from the top-left cell to the bottom-right cell.
+
+
+### Examples
+
+**Example 1:**
+
+
+```
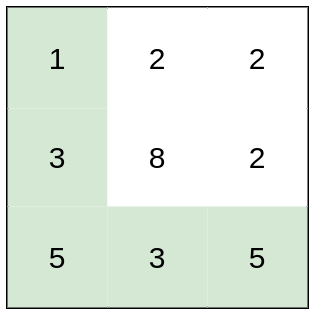
+Input: heights = [[1,2,2],[3,8,2],[5,3,5]]
+Output: 2
+Explanation: The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells.
+This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.
+
+```
+
+**Example 2:**
+
+
+```
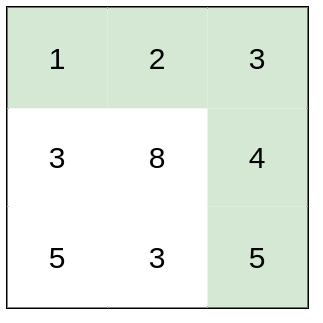
+Input: heights = [[1,2,3],[3,8,4],[5,3,5]]
+Output: 1
+Explanation: The route of [1,2,3,4,5] has a maximum absolute difference of 1 in consecutive cells, which is better than route [1,3,5,3,5].
+```
+
+**Example 3:**
+
+```
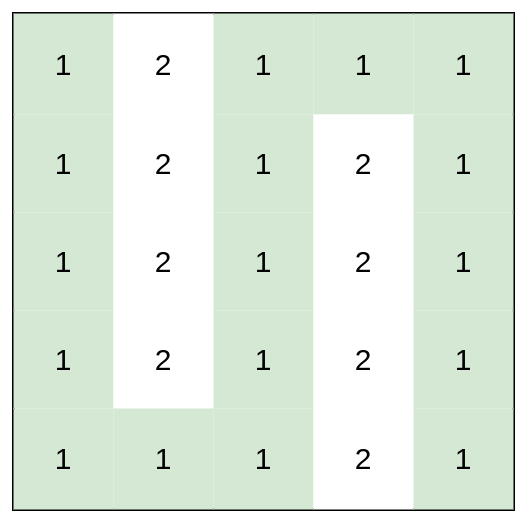
+Input: heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
+Output: 0
+Explanation: This route does not require any effort.
+```
+
+### Constraints
+- `rows == heights.length`
+- `columns == heights[i].length`
+- `1 <= rows, columns <= 100`
+- `1 <= heights[i][j] <= 10^6`
+
+## Solution for Path With Minimum Effort Problem
+### Approach
+#### Dijkstra's Algorithm:
+- A classic algorithm for finding the shortest path in a weighted graph, adapted for this problem.
+
+#### Steps
+##### Initialize Priority Queue:
+- The algorithm starts at the top-left corner (the source). The priority queue is initialized to store the effort needed to reach each cell from the source. The effort for the source itself is zero.
+##### Distance Matrix:
+- A 2D array keeps track of the minimum effort required to reach each cell. Initially, this is set to infinity for all cells except the source.
+
+##### Iterate and Update Distances:
+- The algorithm pops the cell with the smallest effort from the priority queue and explores its neighbors. The effort required to reach a neighbor is updated if a smaller effort is found.
+##### Early Exit:
+- The algorithm stops when it reaches the bottom-right corner, returning the effort required to get there.
+
+
+
+
+
+ #### Implementation
+ ```jsx live
+ function Solution(arr) {
+ function minimumEffortPath(heights) {
+ const rows = heights.length, cols = heights[0].length;
+ const dist = Array.from(Array(rows), () => Array(cols).fill(Infinity));
+ const minHeap = [[0, 0, 0]]; // [effort, x, y]
+
+ dist[0][0] = 0;
+ const directions = [[0, 1], [0, -1], [1, 0], [-1, 0]];
+
+ while (minHeap.length > 0) {
+ const [effort, x, y] = minHeap.shift();
+
+ if (effort > dist[x][y]) continue;
+
+ if (x === rows - 1 && y === cols - 1) return effort;
+
+ for (const [dx, dy] of directions) {
+ const nx = x + dx, ny = y + dy;
+ if (nx >= 0 && nx < rows && ny >= 0 && ny < cols) {
+ const newEffort = Math.max(effort, Math.abs(heights[x][y] - heights[nx][ny]));
+ if (newEffort < dist[nx][ny]) {
+ dist[nx][ny] = newEffort;
+ minHeap.push([newEffort, nx, ny]);
+ minHeap.sort((a, b) => a[0] - b[0]);
+ }
+ }
+ }
+ }
+ return -1;
+ }
+ const input = [[1,2,2],[3,8,2],[5,3,5]]
+ const output = minimumEffortPath(input) ;
+ return (
+
+
+ Input:
+ {JSON.stringify(input)}
+
+
+ Output: {output.toString()}
+
+
+ );
+ }
+ ```
+
+ #### Complexity Analysis
+
+ - Time Complexity: $ O(M*N log(M*N)) $ where M and N are the dimensions of the grid. This is primarily due to the operations on the priority queue.
+ - Space Complexity: $ O(M*N) $ $O(M*N)$, needed for the distance matrix and the priority queue.
+
+ ## Code in Different Languages
+
+
+
+ ```javascript
+ function minimumEffortPath(heights) {
+ const rows = heights.length, cols = heights[0].length;
+ const dist = Array.from(Array(rows), () => Array(cols).fill(Infinity));
+ const minHeap = [[0, 0, 0]]; // [effort, x, y]
+
+ dist[0][0] = 0;
+ const directions = [[0, 1], [0, -1], [1, 0], [-1, 0]];
+
+ while (minHeap.length > 0) {
+ const [effort, x, y] = minHeap.shift();
+
+ if (effort > dist[x][y]) continue;
+
+ if (x === rows - 1 && y === cols - 1) return effort;
+
+ for (const [dx, dy] of directions) {
+ const nx = x + dx, ny = y + dy;
+ if (nx >= 0 && nx < rows && ny >= 0 && ny < cols) {
+ const newEffort = Math.max(effort, Math.abs(heights[x][y] - heights[nx][ny]));
+ if (newEffort < dist[nx][ny]) {
+ dist[nx][ny] = newEffort;
+ minHeap.push([newEffort, nx, ny]);
+ minHeap.sort((a, b) => a[0] - b[0]);
+ }
+ }
+ }
+ }
+ return -1;
+ }
+ ```
+
+
+
+
+ ```typescript
+ class Solution {
+ minimumEffortPath(heights: number[][]): number {
+ const pq = new MinPriorityQueue<{priority: number, element: [number, [number, number]]}>({ priority: x => x.priority });
+ const n = heights.length;
+ const m = heights[0].length;
+ const dist = Array.from({ length: n }, () => Array(m).fill(Infinity));
+ dist[0][0] = 0;
+ pq.enqueue({priority: 0, element: [0, [0, 0]]});
+
+ const delRow = [-1, 0, 1, 0];
+ const delCol = [0, 1, 0, -1];
+
+ while (!pq.isEmpty()) {
+ const {element: [diff, [row, col]]} = pq.dequeue();
+
+ if (row === n - 1 && col === m - 1) return diff;
+
+ for (let i = 0; i < 4; i++) {
+ const newRow = row + delRow[i];
+ const newCol = col + delCol[i];
+
+ if (newRow >= 0 && newRow < n && newCol >= 0 && newCol < m) {
+ const newEffort = Math.max(Math.abs(heights[row][col] - heights[newRow][newCol]), diff);
+ if (newEffort < dist[newRow][newCol]) {
+ dist[newRow][newCol] = newEffort;
+ pq.enqueue({priority: newEffort, element: [newEffort, [newRow, newCol]]});
+ }
+ }
+ }
+ }
+ return 0;
+ }
+}
+
+ ```
+
+
+
+ ```python
+ import heapq
+
+class Solution:
+ def minimumEffortPath(self, heights: List[List[int]]) -> int:
+ n, m = len(heights), len(heights[0])
+ dist = [[float('inf')] * m for _ in range(n)]
+ dist[0][0] = 0
+ pq = [(0, 0, 0)]
+
+ delRow = [-1, 0, 1, 0]
+ delCol = [0, 1, 0, -1]
+
+ while pq:
+ diff, row, col = heapq.heappop(pq)
+
+ if row == n - 1 and col == m - 1:
+ return diff
+
+ for i in range(4):
+ newRow, newCol = row + delRow[i], col + delCol[i]
+
+ if 0 <= newRow < n and 0 <= newCol < m:
+ newEffort = max(abs(heights[row][col] - heights[newRow][newCol]), diff)
+ if newEffort < dist[newRow][newCol]:
+ dist[newRow][newCol] = newEffort
+ heapq.heappush(pq, (newEffort, newRow, newCol))
+ return 0
+
+ ```
+
+
+
+
+ ```java
+ import java.util.*;
+
+class Solution {
+ public int minimumEffortPath(int[][] heights) {
+ PriorityQueue pq = new PriorityQueue<>(Comparator.comparingInt(a -> a[0]));
+ int n = heights.length;
+ int m = heights[0].length;
+ int[][] dist = new int[n][m];
+ for (int[] row : dist) Arrays.fill(row, Integer.MAX_VALUE);
+ dist[0][0] = 0;
+ pq.offer(new int[]{0, 0, 0});
+
+ int[] delRow = {-1, 0, 1, 0};
+ int[] delCol = {0, 1, 0, -1};
+
+ while (!pq.isEmpty()) {
+ int[] curr = pq.poll();
+ int diff = curr[0];
+ int row = curr[1];
+ int col = curr[2];
+
+ if (row == n - 1 && col == m - 1) return diff;
+
+ for (int i = 0; i < 4; i++) {
+ int newRow = row + delRow[i];
+ int newCol = col + delCol[i];
+
+ if (newRow >= 0 && newRow < n && newCol >= 0 && newCol < m) {
+ int newEffort = Math.max(Math.abs(heights[row][col] - heights[newRow][newCol]), diff);
+ if (newEffort < dist[newRow][newCol]) {
+ dist[newRow][newCol] = newEffort;
+ pq.offer(new int[]{newEffort, newRow, newCol});
+ }
+ }
+ }
+ }
+ return 0;
+ }
+}
+
+ ```
+
+
+
+
+ ```cpp
+ class Solution {
+public:
+ int minimumEffortPath(vector>& heights) {
+ priority_queue>,
+ vector>>,
+ greater>>>pq;
+
+ int n = heights.size();
+ int m = heights[0].size();
+
+ vector> dist(n, vector(m, 1e9));
+ dist[0][0] = 0;
+ // {diff{row,col}}
+ pq.push({0, {0, 0}});
+
+ int delRow[] = {-1, 0, 1, 0};
+ int delCol[] = {0, 1, 0, -1};
+
+ while (!pq.empty()) {
+ auto it = pq.top();
+ pq.pop();
+
+ int diff = it.first;
+ int row = it.second.first;
+ int col = it.second.second;
+
+ if (row == n - 1 && col == m - 1)
+ return diff;
+
+ for (int i = 0; i < 4; i++) {
+ int newRow = row + delRow[i];
+ int newCol = col + delCol[i];
+
+ if (newRow >= 0 & newRow < n && newCol >= 0 && newCol < m) {
+ int newEffort = max(
+ abs(heights[row][col] - heights[newRow][newCol]), diff);
+ ;
+ if (newEffort < dist[newRow][newCol]) {
+ dist[newRow][newCol] = newEffort;
+ pq.push({newEffort, {newRow, newCol}});
+ }
+ }
+ }
+ }
+ return 0;
+ }
+};
+ ```
+
+
+
+
+
+
+## References
+
+- **LeetCode Problem**: [Path With Minimum Effort](https://leetcode.com/problems/path-with-minimum-effort/description/)
+
+- **Solution Link**: [LeetCode Solution](https://leetcode.com/problems/path-with-minimum-effort/solutions)
+
From 8f897e7d3c29d4f5d8902014721d72902b10c54f Mon Sep 17 00:00:00 2001
From: Hitesh4278 <97452642+Hitesh4278@users.noreply.github.com>
Date: Fri, 14 Jun 2024 12:35:52 +0000
Subject: [PATCH 3/4] Corrected the path of the file
---
dsa-problems/leetcode-problems/1600-1699.md | 2 +-
1 file changed, 1 insertion(+), 1 deletion(-)
diff --git a/dsa-problems/leetcode-problems/1600-1699.md b/dsa-problems/leetcode-problems/1600-1699.md
index 74937d1b5..63f093c86 100644
--- a/dsa-problems/leetcode-problems/1600-1699.md
+++ b/dsa-problems/leetcode-problems/1600-1699.md
@@ -200,7 +200,7 @@ export const problems = [
"problemName": "1631. Path With Minimum Effort",
"difficulty": "Medium",
"leetCodeLink": "https://leetcode.com/problems/path-with-minimum-effort",
- "solutionLink": "/dsa-solutions/lc-solutions/1600-1631/path-with-minimum-effort"
+ "solutionLink": "/dsa-solutions/lc-solutions/1600-1699/path-with-minimum-effort"
},
{
"problemName": "1632. Rank Transform of a Matrix",
From 97a28cb2a1b6cb71b78ccf4c7a7dcd2e593cdf47 Mon Sep 17 00:00:00 2001
From: Hitesh4278 <97452642+Hitesh4278@users.noreply.github.com>
Date: Fri, 14 Jun 2024 13:14:34 +0000
Subject: [PATCH 4/4] Added the Solution for Tuple With Same Product
---
dsa-problems/leetcode-problems/1700-1799.md | 2 +-
.../1700-1799/1726-tuple-with-same-product.md | 252 ++++++++++++++++++
2 files changed, 253 insertions(+), 1 deletion(-)
create mode 100644 dsa-solutions/lc-solutions/1700-1799/1726-tuple-with-same-product.md
diff --git a/dsa-problems/leetcode-problems/1700-1799.md b/dsa-problems/leetcode-problems/1700-1799.md
index 7ad4657ed..49a16f189 100644
--- a/dsa-problems/leetcode-problems/1700-1799.md
+++ b/dsa-problems/leetcode-problems/1700-1799.md
@@ -170,7 +170,7 @@ export const problems = [
"problemName": "1726. Tuple with Same Product",
"difficulty": "Medium",
"leetCodeLink": "https://leetcode.com/problems/tuple-with-same-product",
- "solutionLink": "#"
+ "solutionLink": "/dsa-solutions/lc-solutions/1700-1799/tuple-with-same-product"
},
{
"problemName": "1727. Largest Submatrix With Rearrangements",
diff --git a/dsa-solutions/lc-solutions/1700-1799/1726-tuple-with-same-product.md b/dsa-solutions/lc-solutions/1700-1799/1726-tuple-with-same-product.md
new file mode 100644
index 000000000..a42b390d7
--- /dev/null
+++ b/dsa-solutions/lc-solutions/1700-1799/1726-tuple-with-same-product.md
@@ -0,0 +1,252 @@
+---
+id: tuple-with-same-product
+title: Tuple with Same Product
+sidebar_label: 1726 - Tuple with Same Product
+tags:
+- Array
+- Hash Table
+- Counting
+
+description: "This is a solution to theTuple with Same Product problem on LeetCode."
+---
+
+## Problem Description
+Given an array nums of distinct positive integers, return the number of tuples (a, b, c, d) such that a * b = c * d where a, b, c, and d are elements of nums, and a != b != c != d.
+
+### Examples
+
+**Example 1:**
+```
+Input: nums = [2,3,4,6]
+Output: 8
+Explanation: There are 8 valid tuples:
+(2,6,3,4) , (2,6,4,3) , (6,2,3,4) , (6,2,4,3)
+(3,4,2,6) , (4,3,2,6) , (3,4,6,2) , (4,3,6,2)
+
+```
+
+**Example 2:**
+
+```
+Input: nums = [1,2,4,5,10]
+Output: 16
+Explanation: There are 16 valid tuples:
+(1,10,2,5) , (1,10,5,2) , (10,1,2,5) , (10,1,5,2)
+(2,5,1,10) , (2,5,10,1) , (5,2,1,10) , (5,2,10,1)
+(2,10,4,5) , (2,10,5,4) , (10,2,4,5) , (10,2,5,4)
+(4,5,2,10) , (4,5,10,2) , (5,4,2,10) , (5,4,10,2)
+```
+
+
+### Constraints
+- `1 <= nums.length <= 1000`
+- `1 <= nums[i] <= 10^4`
+- `All elements in nums are distinct.`
+
+## Solution for Path With Minimum Effort Problem
+### Approach
+#### Brute Force -
+- The first approach that is find all sets of a , b ,c , d by using 4 nested loop . Time Complexity of this approach is very high $ O(N^4)$ which is not feasible
+#### Optimized Approach Using Hashmap
+
+##### Calculate Product Pairs:
+
+- Iterate through each possible pair of elements in the array.
+- For each pair (nums[i], nums[j]), calculate their product.
+- Store the product in a hash map (mp) where the key is the product and the value is the count of pairs that produce this product.
+##### Count Tuples:
+- Iterate through the hash map.
+- For each unique product that appears n times, the number of ways to choose 2 pairs from n pairs is given by the combination formula C(n, 2) = n * (n - 1) / 2.
+- Since each valid tuple of pairs can be permuted in 8 different ways (each pair can be swapped with the other), multiply the result by 8.
+##### Return the Result:
+- Sum up the counts from all unique products to get the total number of valid tuples and multiply by 8.
+
+
+
+
+ #### Implementation
+ ```jsx live
+ function Solution(arr) {
+ var tupleSameProduct = function(nums) {
+ let mp = new Map();
+
+ for (let i = 0; i < nums.length; ++i) {
+ for (let j = i + 1; j < nums.length; ++j) {
+ let product = nums[i] * nums[j];
+ mp.set(product, (mp.get(product) || 0) + 1);
+ }
+ }
+
+ let ans = 0;
+
+ for (let count of mp.values()) {
+ ans += (count * (count - 1)) / 2;
+ }
+
+ return ans * 8;
+ };
+ const input = [2,3,4,6]
+ const output = tupleSameProduct(input)
+ return (
+
+
+ Input:
+ {JSON.stringify(input)}
+
+
+ Output: {output.toString()}
+
+
+ );
+ }
+ ```
+
+ #### Complexity Analysis
+
+ - Time Complexity: $ O(N^2) $
+ - Space Complexity: $ O(N^2)$
+
+ ## Code in Different Languages
+
+
+
+ ```javascript
+ var tupleSameProduct = function(nums) {
+ let mp = new Map();
+
+ for (let i = 0; i < nums.length; ++i) {
+ for (let j = i + 1; j < nums.length; ++j) {
+ let product = nums[i] * nums[j];
+ mp.set(product, (mp.get(product) || 0) + 1);
+ }
+ }
+
+ let ans = 0;
+
+ for (let count of mp.values()) {
+ ans += (count * (count - 1)) / 2;
+ }
+
+ return ans * 8;
+};
+ ```
+
+
+
+
+ ```typescript
+ function tupleSameProduct(nums: number[]): number {
+ let mp = new Map();
+
+ for (let i = 0; i < nums.length; ++i) {
+ for (let j = i + 1; j < nums.length; ++j) {
+ let product = nums[i] * nums[j];
+ mp.set(product, (mp.get(product) || 0) + 1);
+ }
+ }
+
+ let ans = 0;
+
+ for (let count of mp.values()) {
+ ans += (count * (count - 1)) / 2;
+ }
+
+ return ans * 8;
+}
+
+ ```
+
+
+
+ ```python
+ from collections import defaultdict
+
+class Solution:
+ def tupleSameProduct(self, nums: list[int]) -> int:
+ mp = defaultdict(int)
+
+ for i in range(len(nums)):
+ for j in range(i + 1, len(nums)):
+ product = nums[i] * nums[j]
+ mp[product] += 1
+
+ ans = 0
+
+ for count in mp.values():
+ ans += (count * (count - 1)) // 2
+
+ return ans * 8
+
+ ```
+
+
+
+
+ ```java
+ import java.util.HashMap;
+import java.util.Map;
+
+public class Solution {
+ public int tupleSameProduct(int[] nums) {
+ Map mp = new HashMap<>();
+
+ for (int i = 0; i < nums.length; ++i) {
+ for (int j = i + 1; j < nums.length; ++j) {
+ int product = nums[i] * nums[j];
+ mp.put(product, mp.getOrDefault(product, 0) + 1);
+ }
+ }
+
+ int ans = 0;
+
+ for (Map.Entry entry : mp.entrySet()) {
+ int n = entry.getValue();
+ ans += (n * (n - 1)) / 2;
+ }
+
+ return ans * 8;
+ }
+}
+
+ ```
+
+
+
+
+ ```cpp
+ class Solution {
+public:
+ int tupleSameProduct(vector& nums) {
+ unordered_map mp;
+
+ for (int i = 0; i < nums.size(); ++i) {
+ for (int j = i + 1; j < nums.size(); ++j) {
+ int product = nums[i] * nums[j];
+ mp[product]++;
+ }
+ }
+
+ int ans = 0;
+
+ for (auto it = mp.begin(); it != mp.end(); ++it) {
+ int n = it->second;
+ ans += (n * (n - 1)) / 2; // total tuples
+ }
+
+ return ans * 8;
+ }
+};
+
+ ```
+
+
+
+
+
+
+## References
+
+- **LeetCode Problem**: [Tuple With Same Product](https://leetcode.com/problems/tuple-with-same-product/description/)
+
+- **Solution Link**: [LeetCode Solution](https://leetcode.com/problems/tuple-with-same-product/solutions)
+