Merge pull request #1369 from shreyash3087/add/leetcode-593

Docs: Added Solutions to Leetcode 593

Author: ajay-dhangar

dsa-problems/leetcode-problems/0500-0599.md

@@ -488,7 +488,7 @@ export const problems =[
     "problemName": "593. Valid Square",
     "difficulty": "Medium",
     "leetCodeLink": "https://leetcode.com/problems/valid-square",
-    "solutionLink": "#"
+    "solutionLink": "/dsa-solutions/lc-solutions/0500-0599/valid-square"
   },
   {
     "problemName": "594. Longest Harmonious Subsequence",

dsa-solutions/lc-solutions/0500-0599/0593-valid-square.md

@@ -0,0 +1,140 @@
+---
+id: valid-square
+title: Valid Square
+sidebar_label: 0593 - Valid Square
+tags:
+  - Math
+  - Geometry
+  - Sorting
+description: "This is a solution to the Valid Square problem on LeetCode."
+---
+
+## Problem Description
+
+Given the coordinates of four points in 2D space `p1`, `p2`, `p3` and `p4`, return `true` if the four points construct a square.
+
+The coordinate of a point pi is represented as `[xi, yi]`. The input is **not** given in any order.
+
+A **valid square** has four equal sides with positive length and four equal angles (90-degree angles).
+
+### Examples
+**Example 1:**
+
+```
+Input: p1 = [0,0], p2 = [1,1], p3 = [1,0], p4 = [0,1]
+Output: true
+```
+
+**Example 2:**
+
+```
+Input: p1 = [0,0], p2 = [1,1], p3 = [1,0], p4 = [0,12]
+Output: false
+```
+
+### Constraints
+
+- `p1.length == p2.length == p3.length == p4.length == 2`
+- $-10^4 <= xi, yi <= 10^4$
+
+## Solution for Valid Square
+### Approach: Using Sorting
+
+We can make use of maths to simplify this problem a bit. If we sort the given set of points based on their x-coordinate values, and in the case of a tie, based on their y-coordinate value, we can obtain an arrangement, which directly reflects the arrangement of points on a valid square boundary possible.
+
+Consider the only possible cases as shown in the figure below:
+![image](https://assets.leetcode.com/static_assets/media/original_images/593_Valid_Square_1.PNG)
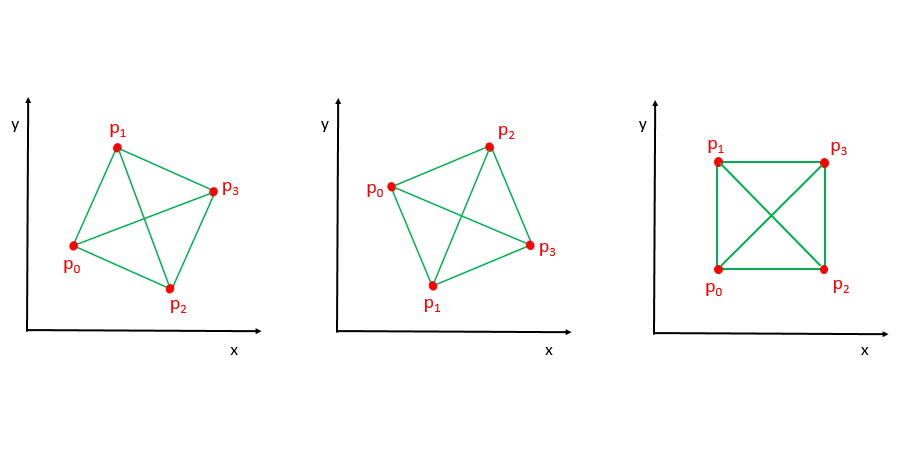+In each case, after sorting, we obtain the following conclusion regarding the connections of the points:
+
+1. p0p1, p1p3, p3p2 and p2p0 form the four sides of any valid square.
+
+2. p0p3 and p1p2 form the diagonals of the square.
+
+Thus, once the sorting of the points is done, based on the above knowledge, we can directly compare p0p1, p1p3, p3p2 and p2p0 or equality of lengths(corresponding to the sides); and p0p3 and p1p2 for equality of lengths(corresponding to the diagonals).
+
+## Code in Different Languages
+
+<Tabs>
+<TabItem value="cpp" label="C++">
+  <SolutionAuthor name="@Shreyash3087"/>
+
+```cpp
+#include <cmath>
+#include <algorithm>
+#include <vector>
+
+class Solution {
+public:
+    double dist(std::vector<int>& p1, std::vector<int>& p2) {
+        return (p2[1] - p1[1]) * (p2[1] - p1[1]) + (p2[0] - p1[0]) * (p2[0] - p1[0]);
+    }
+    bool validSquare(std::vector<int>& p1, std::vector<int>& p2, std::vector<int>& p3, std::vector<int>& p4) {
+        std::vector<std::vector<int>> p = {p1, p2, p3, p4};
+        std::sort(p.begin(), p.end(), [](const std::vector<int>& l1, const std::vector<int>& l2) {
+            return l1[0] != l2[0] ? l1[0] < l2[0] : l1[1] < l2[1];
+        });
+        return dist(p[0], p[1]) != 0 && dist(p[0], p[1]) == dist(p[1], p[3]) && dist(p[1], p[3]) == dist(p[3], p[2]) && dist(p[3], p[2]) == dist(p[2], p[0]) && dist(p[0], p[3]) == dist(p[1], p[2]);
+    }
+};
+
+
+```
+</TabItem>
+<TabItem value="java" label="Java">
+  <SolutionAuthor name="@Shreyash3087"/>
+
+```java
+public class Solution {
+    public double dist(int[] p1, int[] p2) {
+        return (p2[1] - p1[1]) * (p2[1] - p1[1]) + (p2[0] - p1[0]) * (p2[0] - p1[0]);
+    }
+    public boolean validSquare(int[] p1, int[] p2, int[] p3, int[] p4) {
+        int[][] p={p1,p2,p3,p4};
+        Arrays.sort(p, (l1, l2) -> l2[0] == l1[0] ? l1[1] - l2[1] : l1[0] - l2[0]);
+        return dist(p[0], p[1]) != 0 && dist(p[0], p[1]) == dist(p[1], p[3]) && dist(p[1], p[3]) == dist(p[3], p[2]) && dist(p[3], p[2]) == dist(p[2], p[0])   && dist(p[0],p[3])==dist(p[1],p[2]);
+    }
+}
+
+```
+
+</TabItem>
+<TabItem value="python" label="Python">
+  <SolutionAuthor name="@Shreyash3087"/>
+
+```python
+import math
+
+class Solution:
+    def dist(self, p1, p2):
+        return (p2[1] - p1[1]) ** 2 + (p2[0] - p1[0]) ** 2
+
+    def validSquare(self, p1, p2, p3, p4):
+        points = [p1, p2, p3, p4]
+        points.sort(key=lambda x: (x[0], x[1]))
+        
+        return self.dist(points[0], points[1]) != 0 and \
+               self.dist(points[0], points[1]) == self.dist(points[1], points[3]) and \
+               self.dist(points[1], points[3]) == self.dist(points[3], points[2]) and \
+               self.dist(points[3], points[2]) == self.dist(points[2], points[0]) and \
+               self.dist(points[0], points[3]) == self.dist(points[1], points[2])
+
+
+```
+</TabItem>
+</Tabs>
+
+## Complexity Analysis
+
+### Time Complexity: $O(1)$
+
+> **Reason**: Sorting 4 points takes constant time.
+
+### Space Complexity: $O(1)$
+
+> **Reason**: Constant space is required.
+
+## References
+
+- **LeetCode Problem**: [Valid Square](https://leetcode.com/problems/valid-square/description/)
+
+- **Solution Link**: [Valid Square](https://leetcode.com/problems/valid-square/solutions/)