Skip to content

Commit c401e28

Browse files
nishant0708nishant0708
committed
added Q235-236
1 parent c75bd26 commit c401e28

File tree

2 files changed

+311
-0
lines changed

2 files changed

+311
-0
lines changed

‎dsa-solutions/lc-solutions/0200-0299/0235-lowest-common-Ancestor-of-binary-search-tree.md

Lines changed: 165 additions & 0 deletions
Original file line numberDiff line numberDiff line change
@@ -0,0 +1,165 @@
1+
---
2+
id: lowest-common-ancestor-of-a-binary-search-tree.
3+
title: Lowest Common Ancestor of a Binary Search Tree.
4+
sidebar_label: 235-Lowest-Common-Ancestor-of-a-Binary-Search-Tree
5+
tags:
6+
- Binary Search Tree
7+
- Tree
8+
- Depth-First Search
9+
- Binary Tree
10+
description: "Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST."
11+
---
12+
13+
## Problem
14+
15+
Given a binary search tree (BST), find the lowest common ancestor (LCA) node of two given nodes in the BST.
16+
17+
According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”
18+
19+
### Examples
20+
21+
**Example 1:**
22+
23+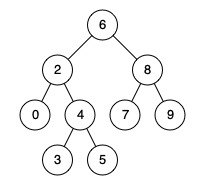
![image](https://assets.leetcode.com/uploads/2018/12/14/binarysearchtree_improved.png)
24+
25+
**Input:** `root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8`
26+
**Output:** `6`
27+
**Explanation:** The LCA of nodes 2 and 8 is 6.
28+
29+
**Example 2:**
30+
31+
![image](https://assets.leetcode.com/uploads/2018/12/14/binarysearchtree_improved.png)
32+
33+
**Input:** `root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4`
34+
**Output:** `2`
35+
**Explanation:** The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
36+
37+
**Example 3:**
38+
39+
**Input:** `root = [2,1], p = 2, q = 1`
40+
**Output:** `2`
41+
42+
### Constraints
43+
44+
- The number of nodes in the tree is in the range `[2, 10^5]`.
45+
- `-10^9 <= Node.val <= 10^9`
46+
- All `Node.val` are unique.
47+
- `p != q`
48+
- `p` and `q` will exist in the BST.
49+
50+
---
51+
52+
## Approach
53+
54+
To find the lowest common ancestor in a Binary Search Tree (BST), we can utilize the properties of the BST. The left subtree of a node contains only nodes with values less than the node's value, and the right subtree contains only nodes with values greater than the node's value.
55+
56+
### Steps:
57+
58+
1. **Start from the Root:** Begin the search from the root node of the BST.
59+
2. **Value Comparison:**
60+
- If both `p` and `q` are smaller than the current node's value, move to the left child.
61+
- If both `p` and `q` are greater than the current node's value, move to the right child.
62+
- If `p` and `q` lie on either side of the current node, or one of them is the current node, then the current node is their LCA.
63+
64+
### Solution
65+
66+
#### Java
67+
68+
```java
69+
/**
70+
* Definition for a binary tree node.
71+
* public class TreeNode {
72+
* int val;
73+
* TreeNode left;
74+
* TreeNode right;
75+
* TreeNode(int x) { val = x; }
76+
* }
77+
*/
78+
class Solution {
79+
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
80+
while (root != null) {
81+
// If both p and q are lesser than root, LCA must be in the left subtree
82+
if (p.val < root.val && q.val < root.val) {
83+
root = root.left;
84+
}
85+
// If both p and q are greater than root, LCA must be in the right subtree
86+
else if (p.val > root.val && q.val > root.val) {
87+
root = root.right;
88+
}
89+
// If p and q lie on either side of root, or one of them is the root, then root is the LCA
90+
else {
91+
return root;
92+
}
93+
}
94+
return null;
95+
}
96+
}
97+
```
98+
#### CPP
99+
```cpp
100+
/**
101+
* Definition for a binary tree node.
102+
* struct TreeNode {
103+
* int val;
104+
* TreeNode *left;
105+
* TreeNode *right;
106+
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
107+
* };
108+
*/
109+
class Solution {
110+
public:
111+
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
112+
while (root != nullptr) {
113+
// If both p and q are lesser than root, LCA must be in the left subtree
114+
if (p->val < root->val && q->val < root->val) {
115+
root = root->left;
116+
}
117+
// If both p and q are greater than root, LCA must be in the right subtree
118+
else if (p->val > root->val && q->val > root->val) {
119+
root = root->right;
120+
}
121+
// If p and q lie on either side of root, or one of them is the root, then root is the LCA
122+
else {
123+
return root;
124+
}
125+
}
126+
return nullptr;
127+
}
128+
};
129+
```
130+
### Python
131+
```python
132+
# Definition for a binary tree node.
133+
class TreeNode:
134+
def __init__(self, x):
135+
self.val = x
136+
self.left = None
137+
self.right = None
138+
139+
class Solution:
140+
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
141+
while root:
142+
# If both p and q are lesser than root, LCA must be in the left subtree
143+
if p.val < root.val and q.val < root.val:
144+
root = root.left
145+
# If both p and q are greater than root, LCA must be in the right subtree
146+
elif p.val > root.val and q.val > root.val:
147+
root = root.right
148+
# If p and q lie on either side of root, or one of them is the root, then root is the LCA
149+
else:
150+
return root
151+
return None
152+
```
153+
154+
### Complexity Analysis
155+
#### Time Complexity: O(h)
156+
157+
**Reason**: The algorithm may traverse the height h of the tree. In the worst case, this is O(log n) for a balanced BST and O(n) for a skewed BST.
158+
Space Complexity: O(1)
159+
160+
**Reason**: The algorithm uses constant space.
161+
#### References
162+
**LeetCode Problem** : Lowest Common Ancestor of a Binary Search Tree
163+
**Solution Link**: LCA Solution on LeetCode
164+
165+
**Wikipedia Definition**: Lowest Common Ancestor

‎dsa-solutions/lc-solutions/0200-0299/0236-Lowest-Common-Ancestor-of-a-Binary-Tree.md

Lines changed: 146 additions & 0 deletions
Original file line numberDiff line numberDiff line change
@@ -0,0 +1,146 @@
1+
---
2+
id: lowest-common-ancestor-of-a-binary-tree
3+
title: Lowest Common Ancestor of a Binary Tree
4+
sidebar_label: 0236-Lowest-Common-Ancestor-of-a-Binary-Tree
5+
tags:
6+
- Tree
7+
- Depth-First Search
8+
- Binary Tree
9+
description: "Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree."
10+
---
11+
12+
## Problem
13+
14+
Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.
15+
16+
According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”
17+
18+
### Examples
19+
20+
**Example 1:**
21+
22+
**Input:** `root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1`
23+
**Output:** `3`
24+
**Explanation:** The LCA of nodes 5 and 1 is 3.
25+
26+
**Example 2:**
27+
28+
**Input:** `root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4`
29+
**Output:** `5`
30+
**Explanation:** The LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.
31+
32+
**Example 3:**
33+
34+
**Input:** `root = [1,2], p = 1, q = 2`
35+
**Output:** `1`
36+
37+
### Constraints
38+
39+
- The number of nodes in the tree is in the range `[2, 10^5]`.
40+
- `-10^9 <= Node.val <= 10^9`
41+
- All `Node.val` are unique.
42+
- `p != q`
43+
- `p` and `q` will exist in the tree.
44+
45+
---
46+
47+
## Approach
48+
49+
To find the lowest common ancestor in a binary tree, we can use a recursive depth-first search (DFS) approach. The idea is to traverse the tree starting from the root. If we find either of the nodes `p` or `q`, we return that node. If both nodes are found in different subtrees of a node, then that node is their lowest common ancestor.
50+
51+
### Steps:
52+
53+
1. **Base Case:** If the current node is `null` or matches `p` or `q`, return the current node.
54+
2. **Recursive Search:**
55+
- Recursively search the left subtree for `p` and `q`.
56+
- Recursively search the right subtree for `p` and `q`.
57+
3. **Determine LCA:**
58+
- If both left and right recursive calls return non-null, the current node is the LCA.
59+
- If only one of the recursive calls returns non-null, that means both nodes are located in the same subtree, so return the non-null result.
60+
61+
### Solution
62+
63+
#### Java
64+
65+
```java
66+
/**
67+
* Definition for a binary tree node.
68+
* public class TreeNode {
69+
* int val;
70+
* TreeNode left;
71+
* TreeNode right;
72+
* TreeNode(int x) { val = x; }
73+
* }
74+
*/
75+
class Solution {
76+
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
77+
if (root == null || root == p || root == q) {
78+
return root;
79+
}
80+
TreeNode left = lowestCommonAncestor(root.left, p, q);
81+
TreeNode right = lowestCommonAncestor(root.right, p, q);
82+
if (left != null && right != null) {
83+
return root;
84+
}
85+
return left != null ? left : right;
86+
}
87+
}
88+
```
89+
### C++
90+
```cpp
91+
/**
92+
* Definition for a binary tree node.
93+
* struct TreeNode {
94+
* int val;
95+
* TreeNode *left;
96+
* TreeNode *right;
97+
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
98+
* };
99+
*/
100+
class Solution {
101+
public:
102+
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
103+
if (root == nullptr || root == p || root == q) {
104+
return root;
105+
}
106+
TreeNode* left = lowestCommonAncestor(root->left, p, q);
107+
TreeNode* right = lowestCommonAncestor(root->right, p, q);
108+
if (left != nullptr && right != nullptr) {
109+
return root;
110+
}
111+
return left != nullptr ? left : right;
112+
}
113+
};
114+
```
115+
### Python
116+
```
117+
# Definition for a binary tree node.
118+
class TreeNode:
119+
def __init__(self, x):
120+
self.val = x
121+
self.left = None
122+
self.right = None
123+
124+
class Solution:
125+
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
126+
if not root or root == p or root == q:
127+
return root
128+
left = self.lowestCommonAncestor(root.left, p, q)
129+
right = self.lowestCommonAncestor(root.right, p, q)
130+
if left and right:
131+
return root
132+
return left if left else right
133+
```
134+
### Complexity Analysis
135+
#### Time Complexity: O(n)
136+
137+
**Reason:** The algorithm visits each node in the tree once, where n is the number of nodes in the tree.
138+
Space Complexity: O(h)
139+
140+
**Reason:** The space complexity is determined by the height h of the tree due to the recursion stack. In the worst case, the height of the tree is O(n) for a skewed tree, but O(log n) for a balanced tree.
141+
142+
### References
143+
**LeetCode Problem:** Lowest Common Ancestor of a Binary Tree
144+
145+
**Solution Link:** LCA Solution on LeetCode
146+
**Wikipedia Definition:** Lowest Common Ancestor

0 commit comments

Comments
 (0)