|
| 1 | +--- |
| 2 | +id: cat-and-mouse |
| 3 | +title: Cat and Mouse |
| 4 | +sidebar_label: 0913 - Cat and Mouse |
| 5 | +tags: |
| 6 | + - Dynamic Programming |
| 7 | + - Depth-First Search |
| 8 | + - Memoization |
| 9 | +description: "This is a solution to the Cat and Mouse problem on LeetCode." |
| 10 | +--- |
| 11 | + |
| 12 | +## Problem Description |
| 13 | + |
| 14 | +A game on an **undirected** graph is played by two players, Mouse and Cat, who alternate turns. |
| 15 | + |
| 16 | +The graph is given as follows: `graph[a]` is a list of all nodes `b` such that `ab` is an edge of the graph. |
| 17 | + |
| 18 | +The mouse starts at node `1` and goes first, the cat starts at node `2` and goes second, and there is a hole at node 0. |
| 19 | + |
| 20 | +During each player's turn, they **must** travel along one edge of the graph that meets where they are. For example, if the Mouse is at node 1, it **must** travel to any node in `graph[1]`. |
| 21 | + |
| 22 | +Additionally, it is not allowed for the Cat to travel to the Hole (node `0`). |
| 23 | + |
| 24 | +Then, the game can end in three ways: |
| 25 | + |
| 26 | +- If ever the Cat occupies the same node as the Mouse, the Cat wins. |
| 27 | +- If ever the Mouse reaches the Hole, the Mouse wins. |
| 28 | +- If ever a position is repeated (i.e., the players are in the same position as a previous turn, and it is the same player's turn to move), the game is a draw. |
| 29 | + |
| 30 | +Given a graph, and assuming both players play optimally, return |
| 31 | + |
| 32 | +- 1 if the mouse wins the game, |
| 33 | +- 2 if the cat wins the game, or |
| 34 | +- 0 if the game is a draw. |
| 35 | + |
| 36 | +### Examples |
| 37 | + |
| 38 | +**Example 1:** |
| 39 | + |
| 40 | +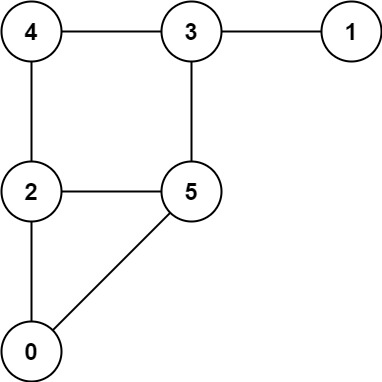 |
| 41 | +``` |
| 42 | +Input: graph = [[2,5],[3],[0,4,5],[1,4,5],[2,3],[0,2,3]] |
| 43 | +Output: 0 |
| 44 | +``` |
| 45 | +**Example 2:** |
| 46 | + |
| 47 | +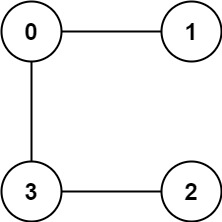 |
| 48 | +``` |
| 49 | +Input: graph = [[1,3],[0],[3],[0,2]] |
| 50 | +Output: 1 |
| 51 | +``` |
| 52 | + |
| 53 | +### Constraints |
| 54 | + |
| 55 | +- `3 <= graph.length <= 50` |
| 56 | +- `1 <= graph[i].length < graph.length` |
| 57 | +- `0 <= graph[i][j] < graph.length` |
| 58 | +- `graph[i][j] != i` |
| 59 | +- `graph[i]` is unique. |
| 60 | +- The mouse and the cat can always move. |
| 61 | + |
| 62 | +## Solution for Cat and Mouse |
| 63 | + |
| 64 | +## Approach: Minimax / Percolate from Resolved States |
| 65 | +### Intuition |
| 66 | + |
| 67 | +The state of the game can be represented as `(m, c, t)` where `m` is the location of the mouse, `c` is the location of the cat, and `t` is 1 if it is the mouse's move, else `2`. Let's call these states nodes. These states form a directed graph: the player whose turn it is has various moves which can be considered as outgoing edges from this node to other nodes. |
| 68 | + |
| 69 | +Some of these nodes are already resolved: if the mouse is at the hole `(m = 0)`, then the mouse wins; if the cat is where the mouse is `(c = m)`, then the cat wins. Let's say that nodes will either be colored MOUSE, CAT, or DRAW depending on which player is assured victory. |
| 70 | + |
| 71 | +As in a standard minimax algorithm, the Mouse player will prefer MOUSE nodes first, DRAW nodes second, and CAT nodes last, and the Cat player prefers these nodes in the opposite order. |
| 72 | + |
| 73 | +### Algorithm |
| 74 | + |
| 75 | +We will color each node marked DRAW according to the following rule. (We'll suppose the node has node.turn = Mouse: the other case is similar.) |
| 76 | + |
| 77 | +- ("Immediate coloring"): If there is a child that is colored $\small\text{MOUSE}$, then this node will also be colored $\small\text{MOUSE}$. |
| 78 | + |
| 79 | +- ("Eventual coloring"): If all children are colored $\small\text{CAT}$, then this node will also be colored $\small\text{CAT}$. |
| 80 | + |
| 81 | +We will repeatedly do this kind of coloring until no node satisfies the above conditions. To perform this coloring efficiently, we will use a queue and perform a bottom-up percolation: |
| 82 | + |
| 83 | +- Enqueue any node initially colored (because the Mouse is at the Hole, or the Cat is at the Mouse.) |
| 84 | + |
| 85 | +- For every node in the queue, for each parent of that node: |
| 86 | + |
| 87 | + - Do an immediate coloring of parent if you can. |
| 88 | + |
| 89 | + - If you can't, then decrement the side-count of the number of children marked $\small\text{DRAW}$. If it becomes zero, then do an "eventual coloring" of this parent. |
| 90 | + |
| 91 | + - All parents that were colored in this manner get enqueued to the queue. |
| 92 | + |
| 93 | +### Proof of Correctness |
| 94 | + |
| 95 | +Our proof is similar to a proof that minimax works. |
| 96 | + |
| 97 | +Say we cannot color any nodes any more, and say from any node colored $\small\text{CAT}$ or $\small\text{MOUSE}$ we need at most K moves to win. If say, some node marked $\small\text{DRAW}$ is actually a win for Mouse, it must have been with $>K$ moves. Then, a path along optimal play (that tries to prolong the loss as long as possible) must arrive at a node colored $\small\text{MOUSE}$ (as eventually the Mouse reaches the Hole.) Thus, there must have been some transition $\small\text{DRAW} \rightarrow \small\text{MOUSE}$ along this path. |
| 98 | + |
| 99 | +If this transition occurred at a `node` with `node.turn = Mouse`, then it breaks our immediate coloring rule. If it occured with `node.turn = Cat`, and all children of node have color $\small\text{MOUSE}$, then it breaks our eventual coloring rule. If some child has color $\small\text{CAT}$, then it breaks our immediate coloring rule. Thus, in this case node will have some child with $\small\text{DRAW}$, which breaks our optimal play assumption, as moving to this child ends the game in $>K$ moves, whereas moving to the colored neighbor ends the game in $\leq K$ moves. |
| 100 | + |
| 101 | +### Code in Different Languages |
| 102 | + |
| 103 | +<Tabs> |
| 104 | +<TabItem value="cpp" label="C++"> |
| 105 | + <SolutionAuthor name="@Shreyash3087"/> |
| 106 | + |
| 107 | +```cpp |
| 108 | +#include <vector> |
| 109 | +#include <queue> |
| 110 | +#include <unordered_map> |
| 111 | + |
| 112 | +class Solution { |
| 113 | +public: |
| 114 | + int catMouseGame(std::vector<std::vector<int>>& graph) { |
| 115 | + int N = graph.size(); |
| 116 | + const int DRAW = 0, MOUSE = 1, CAT = 2; |
| 117 | + |
| 118 | + std::vector<std::vector<std::vector<int>>> color(50, std::vector<std::vector<int>>(50, std::vector<int>(3, DRAW))); |
| 119 | + std::vector<std::vector<std::vector<int>>> degree(50, std::vector<std::vector<int>>(50, std::vector<int>(3, 0))); |
| 120 | + |
| 121 | + // degree[node] : the number of neutral children of this node |
| 122 | + for (int m = 0; m < N; ++m) |
| 123 | + for (int c = 0; c < N; ++c) { |
| 124 | + degree[m][c][1] = graph[m].size(); |
| 125 | + degree[m][c][2] = graph[c].size(); |
| 126 | + for (int x : graph[c]) if (x == 0) { |
| 127 | + degree[m][c][2]--; |
| 128 | + break; |
| 129 | + } |
| 130 | + } |
| 131 | + |
| 132 | + // enqueued : all nodes that are colored |
| 133 | + std::queue<std::vector<int>> queue; |
| 134 | + for (int i = 0; i < N; ++i) |
| 135 | + for (int t = 1; t <= 2; ++t) { |
| 136 | + color[0][i][t] = MOUSE; |
| 137 | + queue.push({0, i, t, MOUSE}); |
| 138 | + if (i > 0) { |
| 139 | + color[i][i][t] = CAT; |
| 140 | + queue.push({i, i, t, CAT}); |
| 141 | + } |
| 142 | + } |
| 143 | + |
| 144 | + // percolate |
| 145 | + while (!queue.empty()) { |
| 146 | + // for nodes that are colored : |
| 147 | + std::vector<int> node = queue.front(); |
| 148 | + queue.pop(); |
| 149 | + int i = node[0], j = node[1], t = node[2], c = node[3]; |
| 150 | + // for every parent of this node i, j, t : |
| 151 | + for (std::vector<int> parent : parents(graph, i, j, t)) { |
| 152 | + int i2 = parent[0], j2 = parent[1], t2 = parent[2]; |
| 153 | + // if this parent is not colored : |
| 154 | + if (color[i2][j2][t2] == DRAW) { |
| 155 | + // if the parent can make a winning move (ie. mouse to MOUSE), do so |
| 156 | + if (t2 == c) { |
| 157 | + color[i2][j2][t2] = c; |
| 158 | + queue.push({i2, j2, t2, c}); |
| 159 | + } else { |
| 160 | + // else, this parent has degree[parent]--, and enqueue |
| 161 | + // if all children of this parent are colored as losing moves |
| 162 | + degree[i2][j2][t2]--; |
| 163 | + if (degree[i2][j2][t2] == 0) { |
| 164 | + color[i2][j2][t2] = 3 - t2; |
| 165 | + queue.push({i2, j2, t2, 3 - t2}); |
| 166 | + } |
| 167 | + } |
| 168 | + } |
| 169 | + } |
| 170 | + } |
| 171 | + |
| 172 | + return color[1][2][1]; |
| 173 | + } |
| 174 | + |
| 175 | + // What nodes could play their turn to |
| 176 | + // arrive at node (m, c, t) ? |
| 177 | + std::vector<std::vector<int>> parents(std::vector<std::vector<int>>& graph, int m, int c, int t) { |
| 178 | + std::vector<std::vector<int>> ans; |
| 179 | + if (t == 2) { |
| 180 | + for (int m2 : graph[m]) |
| 181 | + ans.push_back({m2, c, 3-t}); |
| 182 | + } else { |
| 183 | + for (int c2 : graph[c]) if (c2 > 0) |
| 184 | + ans.push_back({m, c2, 3-t}); |
| 185 | + } |
| 186 | + return ans; |
| 187 | + } |
| 188 | +}; |
| 189 | + |
| 190 | + |
| 191 | +``` |
| 192 | +</TabItem> |
| 193 | +<TabItem value="java" label="Java"> |
| 194 | + <SolutionAuthor name="@Shreyash3087"/> |
| 195 | + |
| 196 | +```java |
| 197 | +class Solution { |
| 198 | + public int catMouseGame(int[][] graph) { |
| 199 | + int N = graph.length; |
| 200 | + final int DRAW = 0, MOUSE = 1, CAT = 2; |
| 201 | + |
| 202 | + int[][][] color = new int[50][50][3]; |
| 203 | + int[][][] degree = new int[50][50][3]; |
| 204 | + |
| 205 | + // degree[node] : the number of neutral children of this node |
| 206 | + for (int m = 0; m < N; ++m) |
| 207 | + for (int c = 0; c < N; ++c) { |
| 208 | + degree[m][c][1] = graph[m].length; |
| 209 | + degree[m][c][2] = graph[c].length; |
| 210 | + for (int x: graph[c]) if (x == 0) { |
| 211 | + degree[m][c][2]--; |
| 212 | + break; |
| 213 | + } |
| 214 | + } |
| 215 | + |
| 216 | + // enqueued : all nodes that are colored |
| 217 | + Queue<int[]> queue = new LinkedList(); |
| 218 | + for (int i = 0; i < N; ++i) |
| 219 | + for (int t = 1; t <= 2; ++t) { |
| 220 | + color[0][i][t] = MOUSE; |
| 221 | + queue.add(new int[]{0, i, t, MOUSE}); |
| 222 | + if (i > 0) { |
| 223 | + color[i][i][t] = CAT; |
| 224 | + queue.add(new int[]{i, i, t, CAT}); |
| 225 | + } |
| 226 | + } |
| 227 | + |
| 228 | + // percolate |
| 229 | + while (!queue.isEmpty()) { |
| 230 | + // for nodes that are colored : |
| 231 | + int[] node = queue.remove(); |
| 232 | + int i = node[0], j = node[1], t = node[2], c = node[3]; |
| 233 | + // for every parent of this node i, j, t : |
| 234 | + for (int[] parent: parents(graph, i, j, t)) { |
| 235 | + int i2 = parent[0], j2 = parent[1], t2 = parent[2]; |
| 236 | + // if this parent is not colored : |
| 237 | + if (color[i2][j2][t2] == DRAW) { |
| 238 | + // if the parent can make a winning move (ie. mouse to MOUSE), do so |
| 239 | + if (t2 == c) { |
| 240 | + color[i2][j2][t2] = c; |
| 241 | + queue.add(new int[]{i2, j2, t2, c}); |
| 242 | + } else { |
| 243 | + // else, this parent has degree[parent]--, and enqueue |
| 244 | + // if all children of this parent are colored as losing moves |
| 245 | + degree[i2][j2][t2]--; |
| 246 | + if (degree[i2][j2][t2] == 0) { |
| 247 | + color[i2][j2][t2] = 3 - t2; |
| 248 | + queue.add(new int[]{i2, j2, t2, 3 - t2}); |
| 249 | + } |
| 250 | + } |
| 251 | + } |
| 252 | + } |
| 253 | + } |
| 254 | + |
| 255 | + return color[1][2][1]; |
| 256 | + } |
| 257 | + |
| 258 | + // What nodes could play their turn to |
| 259 | + // arrive at node (m, c, t) ? |
| 260 | + public List<int[]> parents(int[][] graph, int m, int c, int t) { |
| 261 | + List<int[]> ans = new ArrayList(); |
| 262 | + if (t == 2) { |
| 263 | + for (int m2: graph[m]) |
| 264 | + ans.add(new int[]{m2, c, 3-t}); |
| 265 | + } else { |
| 266 | + for (int c2: graph[c]) if (c2 > 0) |
| 267 | + ans.add(new int[]{m, c2, 3-t}); |
| 268 | + } |
| 269 | + return ans; |
| 270 | + } |
| 271 | +} |
| 272 | +``` |
| 273 | + |
| 274 | +</TabItem> |
| 275 | +<TabItem value="python" label="Python"> |
| 276 | + <SolutionAuthor name="@Shreyash3087"/> |
| 277 | + |
| 278 | +```python |
| 279 | +class Solution(object): |
| 280 | + def catMouseGame(self, graph): |
| 281 | + N = len(graph) |
| 282 | + |
| 283 | + # What nodes could play their turn to |
| 284 | + # arrive at node (m, c, t) ? |
| 285 | + def parents(m, c, t): |
| 286 | + if t == 2: |
| 287 | + for m2 in graph[m]: |
| 288 | + yield m2, c, 3-t |
| 289 | + else: |
| 290 | + for c2 in graph[c]: |
| 291 | + if c2: |
| 292 | + yield m, c2, 3-t |
| 293 | + |
| 294 | + DRAW, MOUSE, CAT = 0, 1, 2 |
| 295 | + color = collections.defaultdict(int) |
| 296 | + |
| 297 | + # degree[node] : the number of neutral children of this node |
| 298 | + degree = {} |
| 299 | + for m in xrange(N): |
| 300 | + for c in xrange(N): |
| 301 | + degree[m,c,1] = len(graph[m]) |
| 302 | + degree[m,c,2] = len(graph[c]) - (0 in graph[c]) |
| 303 | + |
| 304 | + # enqueued : all nodes that are colored |
| 305 | + queue = collections.deque([]) |
| 306 | + for i in xrange(N): |
| 307 | + for t in xrange(1, 3): |
| 308 | + color[0, i, t] = MOUSE |
| 309 | + queue.append((0, i, t, MOUSE)) |
| 310 | + if i > 0: |
| 311 | + color[i, i, t] = CAT |
| 312 | + queue.append((i, i, t, CAT)) |
| 313 | + |
| 314 | + # percolate |
| 315 | + while queue: |
| 316 | + # for nodes that are colored : |
| 317 | + i, j, t, c = queue.popleft() |
| 318 | + # for every parent of this node i, j, t : |
| 319 | + for i2, j2, t2 in parents(i, j, t): |
| 320 | + # if this parent is not colored : |
| 321 | + if color[i2, j2, t2] is DRAW: |
| 322 | + # if the parent can make a winning move (ie. mouse to MOUSE), do so |
| 323 | + if t2 == c: # winning move |
| 324 | + color[i2, j2, t2] = c |
| 325 | + queue.append((i2, j2, t2, c)) |
| 326 | + # else, this parent has degree[parent]--, and enqueue if all children |
| 327 | + # of this parent are colored as losing moves |
| 328 | + else: |
| 329 | + degree[i2, j2, t2] -= 1 |
| 330 | + if degree[i2, j2, t2] == 0: |
| 331 | + color[i2, j2, t2] = 3 - t2 |
| 332 | + queue.append((i2, j2, t2, 3 - t2)) |
| 333 | + |
| 334 | + return color[1, 2, 1] |
| 335 | +``` |
| 336 | +</TabItem> |
| 337 | +</Tabs> |
| 338 | + |
| 339 | +### Complexity Analysis |
| 340 | + |
| 341 | +#### Time Complexity: $O(N^3)$ |
| 342 | + |
| 343 | +> **Reason**: where N is the number of nodes in the graph. There are $O(N^2)$ states, and each state has an outdegree of N, as there are at most N different moves. |
| 344 | +
|
| 345 | +#### Space Complexity: $O(N^2)$ |
| 346 | + |
| 347 | +> **Reason**:due to the storage requirements of the color and degree arrays, which both have dimensions `[N][N][3]`. |
| 348 | +
|
| 349 | + |
| 350 | +## Video Solution |
| 351 | + |
| 352 | +<LiteYouTubeEmbed |
| 353 | + id="oGKnucI_ejw" |
| 354 | + params="autoplay=1&autohide=1&showinfo=0&rel=0" |
| 355 | + title="LeetCode 913. Cat and Mouse" |
| 356 | + poster="hqdefault" |
| 357 | + webp /> |
| 358 | + |
| 359 | +## References |
| 360 | + |
| 361 | +- **LeetCode Problem**: [Cat and Mouse](https://leetcode.com/problems/cat-and-mouse/description/) |
| 362 | + |
| 363 | +- **Solution Link**: [Cat and Mouse](https://leetcode.com/problems/cat-and-mouse/solutions/) |
0 commit comments