|
| 1 | +--- |
| 2 | +id: path-with-minimum-effort |
| 3 | +title: Path With Minimum Effort |
| 4 | +sidebar_label: 1631 - Path With Minimum Effort |
| 5 | +tags: |
| 6 | +- Array |
| 7 | +- Binary Search |
| 8 | +- Depth-First Search |
| 9 | +- Breadth-First Search |
| 10 | +- Union Find |
| 11 | +- Heap (Priority Queue) |
| 12 | +- Matrix |
| 13 | + |
| 14 | +description: "This is a solution to the Path With Minimum Effort problem on LeetCode." |
| 15 | +--- |
| 16 | + |
| 17 | +## Problem Description |
| 18 | +You are a hiker preparing for an upcoming hike. You are given heights, a 2D array of size rows x columns, where `heights[row][col]` represents the height of cell (row, col). You are situated in the top-left cell, `(0, 0)`, and you hope to travel to the bottom-right cell, `(rows-1, columns-1) (i.e., 0-indexed)`. You can move up, down, left, or right, and you wish to find a route that requires the minimum effort. |
| 19 | + |
| 20 | +A route's effort is the maximum absolute difference in heights between two consecutive cells of the route. |
| 21 | + |
| 22 | +Return the minimum effort required to travel from the top-left cell to the bottom-right cell. |
| 23 | + |
| 24 | + |
| 25 | +### Examples |
| 26 | + |
| 27 | +**Example 1:** |
| 28 | +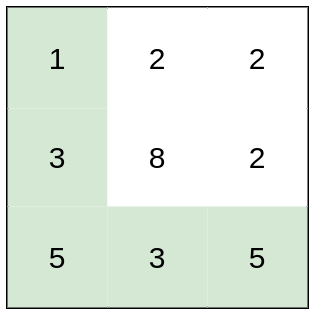 |
| 29 | + |
| 30 | +``` |
| 31 | +Input: heights = [[1,2,2],[3,8,2],[5,3,5]] |
| 32 | +Output: 2 |
| 33 | +Explanation: The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells. |
| 34 | +This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3. |
| 35 | +
|
| 36 | +``` |
| 37 | + |
| 38 | +**Example 2:** |
| 39 | +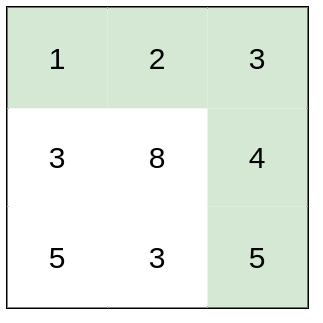 |
| 40 | + |
| 41 | +``` |
| 42 | +Input: heights = [[1,2,3],[3,8,4],[5,3,5]] |
| 43 | +Output: 1 |
| 44 | +Explanation: The route of [1,2,3,4,5] has a maximum absolute difference of 1 in consecutive cells, which is better than route [1,3,5,3,5]. |
| 45 | +``` |
| 46 | + |
| 47 | +**Example 3:** |
| 48 | +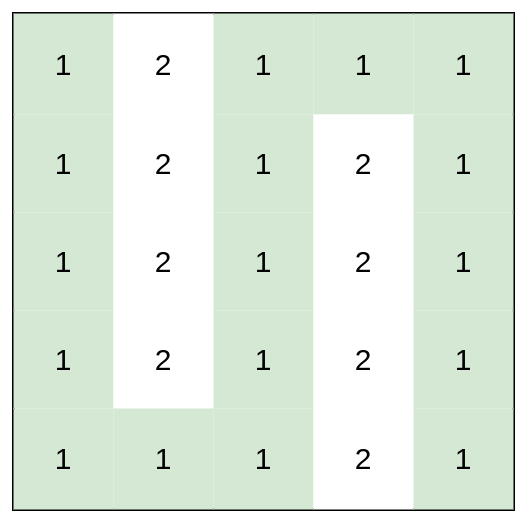 |
| 49 | +``` |
| 50 | +Input: heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]] |
| 51 | +Output: 0 |
| 52 | +Explanation: This route does not require any effort. |
| 53 | +``` |
| 54 | + |
| 55 | +### Constraints |
| 56 | +- `rows == heights.length` |
| 57 | +- `columns == heights[i].length` |
| 58 | +- `1 <= rows, columns <= 100` |
| 59 | +- `1 <= heights[i][j] <= 10^6` |
| 60 | + |
| 61 | +## Solution for Path With Minimum Effort Problem |
| 62 | +### Approach |
| 63 | +#### Dijkstra's Algorithm: |
| 64 | +- A classic algorithm for finding the shortest path in a weighted graph, adapted for this problem. |
| 65 | + |
| 66 | +#### Steps |
| 67 | +##### Initialize Priority Queue: |
| 68 | +- The algorithm starts at the top-left corner (the source). The priority queue is initialized to store the effort needed to reach each cell from the source. The effort for the source itself is zero. |
| 69 | +##### Distance Matrix: |
| 70 | +- A 2D array keeps track of the minimum effort required to reach each cell. Initially, this is set to infinity for all cells except the source. |
| 71 | + |
| 72 | +##### Iterate and Update Distances: |
| 73 | +- The algorithm pops the cell with the smallest effort from the priority queue and explores its neighbors. The effort required to reach a neighbor is updated if a smaller effort is found. |
| 74 | +##### Early Exit: |
| 75 | +- The algorithm stops when it reaches the bottom-right corner, returning the effort required to get there. |
| 76 | + |
| 77 | + |
| 78 | +<Tabs> |
| 79 | + <TabItem value="Solution" label="Solution"> |
| 80 | + |
| 81 | + #### Implementation |
| 82 | + ```jsx live |
| 83 | + function Solution(arr) { |
| 84 | + function minimumEffortPath(heights) { |
| 85 | + const rows = heights.length, cols = heights[0].length; |
| 86 | + const dist = Array.from(Array(rows), () => Array(cols).fill(Infinity)); |
| 87 | + const minHeap = [[0, 0, 0]]; // [effort, x, y] |
| 88 | + |
| 89 | + dist[0][0] = 0; |
| 90 | + const directions = [[0, 1], [0, -1], [1, 0], [-1, 0]]; |
| 91 | + |
| 92 | + while (minHeap.length > 0) { |
| 93 | + const [effort, x, y] = minHeap.shift(); |
| 94 | + |
| 95 | + if (effort > dist[x][y]) continue; |
| 96 | + |
| 97 | + if (x === rows - 1 && y === cols - 1) return effort; |
| 98 | + |
| 99 | + for (const [dx, dy] of directions) { |
| 100 | + const nx = x + dx, ny = y + dy; |
| 101 | + if (nx >= 0 && nx < rows && ny >= 0 && ny < cols) { |
| 102 | + const newEffort = Math.max(effort, Math.abs(heights[x][y] - heights[nx][ny])); |
| 103 | + if (newEffort < dist[nx][ny]) { |
| 104 | + dist[nx][ny] = newEffort; |
| 105 | + minHeap.push([newEffort, nx, ny]); |
| 106 | + minHeap.sort((a, b) => a[0] - b[0]); |
| 107 | + } |
| 108 | + } |
| 109 | + } |
| 110 | + } |
| 111 | + return -1; |
| 112 | + } |
| 113 | + const input = [[1,2,2],[3,8,2],[5,3,5]] |
| 114 | + const output = minimumEffortPath(input) ; |
| 115 | + return ( |
| 116 | + <div> |
| 117 | + <p> |
| 118 | + <b>Input: </b> |
| 119 | + {JSON.stringify(input)} |
| 120 | + </p> |
| 121 | + <p> |
| 122 | + <b>Output:</b> {output.toString()} |
| 123 | + </p> |
| 124 | + </div> |
| 125 | + ); |
| 126 | + } |
| 127 | + ``` |
| 128 | + |
| 129 | + #### Complexity Analysis |
| 130 | + |
| 131 | + - Time Complexity: $ O(M*N log(M*N)) $ where M and N are the dimensions of the grid. This is primarily due to the operations on the priority queue. |
| 132 | + - Space Complexity: $ O(M*N) $ $O(M*N)$, needed for the distance matrix and the priority queue. |
| 133 | + |
| 134 | + ## Code in Different Languages |
| 135 | + <Tabs> |
| 136 | + <TabItem value="JavaScript" label="JavaScript"> |
| 137 | + <SolutionAuthor name="@hiteshgahanolia"/> |
| 138 | + ```javascript |
| 139 | + function minimumEffortPath(heights) { |
| 140 | + const rows = heights.length, cols = heights[0].length; |
| 141 | + const dist = Array.from(Array(rows), () => Array(cols).fill(Infinity)); |
| 142 | + const minHeap = [[0, 0, 0]]; // [effort, x, y] |
| 143 | + |
| 144 | + dist[0][0] = 0; |
| 145 | + const directions = [[0, 1], [0, -1], [1, 0], [-1, 0]]; |
| 146 | + |
| 147 | + while (minHeap.length > 0) { |
| 148 | + const [effort, x, y] = minHeap.shift(); |
| 149 | + |
| 150 | + if (effort > dist[x][y]) continue; |
| 151 | + |
| 152 | + if (x === rows - 1 && y === cols - 1) return effort; |
| 153 | + |
| 154 | + for (const [dx, dy] of directions) { |
| 155 | + const nx = x + dx, ny = y + dy; |
| 156 | + if (nx >= 0 && nx < rows && ny >= 0 && ny < cols) { |
| 157 | + const newEffort = Math.max(effort, Math.abs(heights[x][y] - heights[nx][ny])); |
| 158 | + if (newEffort < dist[nx][ny]) { |
| 159 | + dist[nx][ny] = newEffort; |
| 160 | + minHeap.push([newEffort, nx, ny]); |
| 161 | + minHeap.sort((a, b) => a[0] - b[0]); |
| 162 | + } |
| 163 | + } |
| 164 | + } |
| 165 | + } |
| 166 | + return -1; |
| 167 | + } |
| 168 | + ``` |
| 169 | + |
| 170 | + </TabItem> |
| 171 | + <TabItem value="TypeScript" label="TypeScript"> |
| 172 | + <SolutionAuthor name="@hiteshgahanolia"/> |
| 173 | + ```typescript |
| 174 | + class Solution { |
| 175 | + minimumEffortPath(heights: number[][]): number { |
| 176 | + const pq = new MinPriorityQueue<{priority: number, element: [number, [number, number]]}>({ priority: x => x.priority }); |
| 177 | + const n = heights.length; |
| 178 | + const m = heights[0].length; |
| 179 | + const dist = Array.from({ length: n }, () => Array(m).fill(Infinity)); |
| 180 | + dist[0][0] = 0; |
| 181 | + pq.enqueue({priority: 0, element: [0, [0, 0]]}); |
| 182 | + |
| 183 | + const delRow = [-1, 0, 1, 0]; |
| 184 | + const delCol = [0, 1, 0, -1]; |
| 185 | + |
| 186 | + while (!pq.isEmpty()) { |
| 187 | + const {element: [diff, [row, col]]} = pq.dequeue(); |
| 188 | + |
| 189 | + if (row === n - 1 && col === m - 1) return diff; |
| 190 | + |
| 191 | + for (let i = 0; i < 4; i++) { |
| 192 | + const newRow = row + delRow[i]; |
| 193 | + const newCol = col + delCol[i]; |
| 194 | + |
| 195 | + if (newRow >= 0 && newRow < n && newCol >= 0 && newCol < m) { |
| 196 | + const newEffort = Math.max(Math.abs(heights[row][col] - heights[newRow][newCol]), diff); |
| 197 | + if (newEffort < dist[newRow][newCol]) { |
| 198 | + dist[newRow][newCol] = newEffort; |
| 199 | + pq.enqueue({priority: newEffort, element: [newEffort, [newRow, newCol]]}); |
| 200 | + } |
| 201 | + } |
| 202 | + } |
| 203 | + } |
| 204 | + return 0; |
| 205 | + } |
| 206 | +} |
| 207 | +
|
| 208 | + ``` |
| 209 | + </TabItem> |
| 210 | + <TabItem value="Python" label="Python"> |
| 211 | + <SolutionAuthor name="@hiteshgahanolia"/> |
| 212 | + ```python |
| 213 | + import heapq |
| 214 | +
|
| 215 | +class Solution: |
| 216 | + def minimumEffortPath(self, heights: List[List[int]]) -> int: |
| 217 | + n, m = len(heights), len(heights[0]) |
| 218 | + dist = [[float('inf')] * m for _ in range(n)] |
| 219 | + dist[0][0] = 0 |
| 220 | + pq = [(0, 0, 0)] |
| 221 | + |
| 222 | + delRow = [-1, 0, 1, 0] |
| 223 | + delCol = [0, 1, 0, -1] |
| 224 | + |
| 225 | + while pq: |
| 226 | + diff, row, col = heapq.heappop(pq) |
| 227 | + |
| 228 | + if row == n - 1 and col == m - 1: |
| 229 | + return diff |
| 230 | + |
| 231 | + for i in range(4): |
| 232 | + newRow, newCol = row + delRow[i], col + delCol[i] |
| 233 | + |
| 234 | + if 0 <= newRow < n and 0 <= newCol < m: |
| 235 | + newEffort = max(abs(heights[row][col] - heights[newRow][newCol]), diff) |
| 236 | + if newEffort < dist[newRow][newCol]: |
| 237 | + dist[newRow][newCol] = newEffort |
| 238 | + heapq.heappush(pq, (newEffort, newRow, newCol)) |
| 239 | + return 0 |
| 240 | +
|
| 241 | + ``` |
| 242 | + |
| 243 | + </TabItem> |
| 244 | + <TabItem value="Java" label="Java"> |
| 245 | + <SolutionAuthor name="@hiteshgahanolia"/> |
| 246 | + ```java |
| 247 | + import java.util.*; |
| 248 | +
|
| 249 | +class Solution { |
| 250 | + public int minimumEffortPath(int[][] heights) { |
| 251 | + PriorityQueue<int[]> pq = new PriorityQueue<>(Comparator.comparingInt(a -> a[0])); |
| 252 | + int n = heights.length; |
| 253 | + int m = heights[0].length; |
| 254 | + int[][] dist = new int[n][m]; |
| 255 | + for (int[] row : dist) Arrays.fill(row, Integer.MAX_VALUE); |
| 256 | + dist[0][0] = 0; |
| 257 | + pq.offer(new int[]{0, 0, 0}); |
| 258 | + |
| 259 | + int[] delRow = {-1, 0, 1, 0}; |
| 260 | + int[] delCol = {0, 1, 0, -1}; |
| 261 | + |
| 262 | + while (!pq.isEmpty()) { |
| 263 | + int[] curr = pq.poll(); |
| 264 | + int diff = curr[0]; |
| 265 | + int row = curr[1]; |
| 266 | + int col = curr[2]; |
| 267 | + |
| 268 | + if (row == n - 1 && col == m - 1) return diff; |
| 269 | + |
| 270 | + for (int i = 0; i < 4; i++) { |
| 271 | + int newRow = row + delRow[i]; |
| 272 | + int newCol = col + delCol[i]; |
| 273 | + |
| 274 | + if (newRow >= 0 && newRow < n && newCol >= 0 && newCol < m) { |
| 275 | + int newEffort = Math.max(Math.abs(heights[row][col] - heights[newRow][newCol]), diff); |
| 276 | + if (newEffort < dist[newRow][newCol]) { |
| 277 | + dist[newRow][newCol] = newEffort; |
| 278 | + pq.offer(new int[]{newEffort, newRow, newCol}); |
| 279 | + } |
| 280 | + } |
| 281 | + } |
| 282 | + } |
| 283 | + return 0; |
| 284 | + } |
| 285 | +} |
| 286 | +
|
| 287 | + ``` |
| 288 | + |
| 289 | + </TabItem> |
| 290 | + <TabItem value="C++" label="C++"> |
| 291 | + <SolutionAuthor name="@hiteshgahanolia"/> |
| 292 | + ```cpp |
| 293 | + class Solution { |
| 294 | +public: |
| 295 | + int minimumEffortPath(vector<vector<int>>& heights) { |
| 296 | + priority_queue<pair<int, pair<int, int>>, |
| 297 | + vector<pair<int, pair<int, int>>>, |
| 298 | + greater<pair<int, pair<int, int>>>>pq; |
| 299 | +
|
| 300 | + int n = heights.size(); |
| 301 | + int m = heights[0].size(); |
| 302 | +
|
| 303 | + vector<vector<int>> dist(n, vector<int>(m, 1e9)); |
| 304 | + dist[0][0] = 0; |
| 305 | + // {diff{row,col}} |
| 306 | + pq.push({0, {0, 0}}); |
| 307 | +
|
| 308 | + int delRow[] = {-1, 0, 1, 0}; |
| 309 | + int delCol[] = {0, 1, 0, -1}; |
| 310 | +
|
| 311 | + while (!pq.empty()) { |
| 312 | + auto it = pq.top(); |
| 313 | + pq.pop(); |
| 314 | +
|
| 315 | + int diff = it.first; |
| 316 | + int row = it.second.first; |
| 317 | + int col = it.second.second; |
| 318 | +
|
| 319 | + if (row == n - 1 && col == m - 1) |
| 320 | + return diff; |
| 321 | +
|
| 322 | + for (int i = 0; i < 4; i++) { |
| 323 | + int newRow = row + delRow[i]; |
| 324 | + int newCol = col + delCol[i]; |
| 325 | +
|
| 326 | + if (newRow >= 0 & newRow < n && newCol >= 0 && newCol < m) { |
| 327 | + int newEffort = max( |
| 328 | + abs(heights[row][col] - heights[newRow][newCol]), diff); |
| 329 | + ; |
| 330 | + if (newEffort < dist[newRow][newCol]) { |
| 331 | + dist[newRow][newCol] = newEffort; |
| 332 | + pq.push({newEffort, {newRow, newCol}}); |
| 333 | + } |
| 334 | + } |
| 335 | + } |
| 336 | + } |
| 337 | + return 0; |
| 338 | + } |
| 339 | +}; |
| 340 | + ``` |
| 341 | +</TabItem> |
| 342 | +</Tabs> |
| 343 | + |
| 344 | + </TabItem> |
| 345 | +</Tabs> |
| 346 | + |
| 347 | +## References |
| 348 | + |
| 349 | +- **LeetCode Problem**: [Path With Minimum Effort](https://leetcode.com/problems/path-with-minimum-effort/description/) |
| 350 | + |
| 351 | +- **Solution Link**: [LeetCode Solution](https://leetcode.com/problems/path-with-minimum-effort/solutions) |
| 352 | + |
0 commit comments