|
| 1 | +# Scikit-Learn |
| 2 | + |
| 3 | +> Unlock the Power of Machine Learning with Scikit-learn: Simplifying Complexity, Empowering Discovery |
| 4 | +
|
| 5 | + |
| 6 | +**Supervised Learning** |
| 7 | +- Linear Models |
| 8 | + |
| 9 | +- Support Vector Machines |
| 10 | + |
| 11 | +- Data Preprocessing |
| 12 | + |
| 13 | +1. Linear Models |
| 14 | + |
| 15 | +The following are a set of |
| 16 | +methods intended for regression in which the target value is expected to |
| 17 | +be a linear combination of the features. In mathematical notation, if |
| 18 | +$\hat{y}$ is the predicted value. |
| 19 | + |
| 20 | +$$ |
| 21 | +\hat{y}(w, x) = w_0 + w_1 + \ldots + w_p |
| 22 | +$$ |
| 23 | + |
| 24 | +Across the module, we designate the vector w = |
| 25 | +$(w_0, w_1, \ldots, w_n)$ as `coef_` and $w_0$ as `intercept_`. |
| 26 | + |
| 27 | + |
| 28 | +- *Linear Regression* |
| 29 | + Linear Regression fits a linear model with coefficients w = $(w_0 ,w_1 , |
| 30 | +...w_n)$ to minimize the residual sum of squares between the observed |
| 31 | +targets in the dataset, and the targets predicted by the linear |
| 32 | +approximation. Mathematically it solves a problem of the form: |
| 33 | + |
| 34 | + $\min_{w} || X w - y||_2^2$ |
| 35 | + |
| 36 | +``` python |
| 37 | +from sklearn import linear_model |
| 38 | +reg = linear_model.LinearRegression() #To Use Linear Regression |
| 39 | +reg.fit([[0, 0], [1, 1], [2, 2]], [0, 1, 2]) |
| 40 | +coefficients = reg.coef_ |
| 41 | +intercept = reg.intercept_ |
| 42 | + |
| 43 | +print("Coefficients:", coefficients) |
| 44 | +print("Intercept:", intercept) |
| 45 | +``` |
| 46 | + |
| 47 | +Output: |
| 48 | + |
| 49 | + Coefficients: [0.5 0.5] |
| 50 | + Intercept: 1.1102230246251565e-16 |
| 51 | + |
| 52 | + |
| 53 | +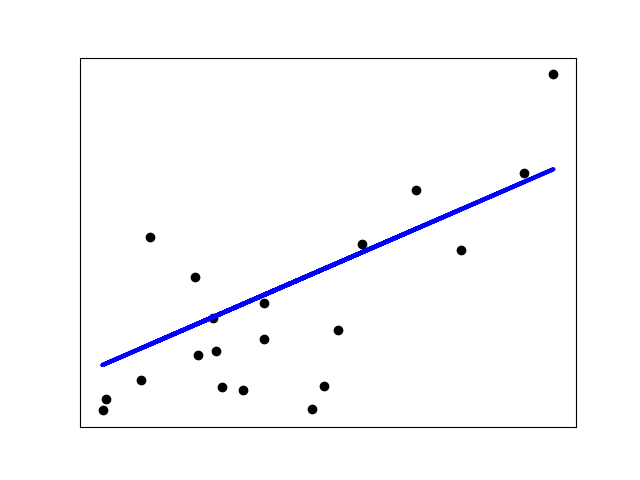 |
| 54 | + |
| 55 | +This is how the Linear Regression fits the line . |
| 56 | + |
| 57 | + |
| 58 | +- Support Vector Machines |
| 59 | + Support vector machines (SVMs) are a set of supervised learning methods |
| 60 | +used for classification, regression and outliers detection. |
| 61 | + |
| 62 | +*The advantages of support vector machines are:* |
| 63 | + |
| 64 | +Effective in high dimensional spaces. |
| 65 | + |
| 66 | +Still effective in cases where number of dimensions is greater than the |
| 67 | +number of samples. |
| 68 | + |
| 69 | +Uses a subset of training points in the decision function (called |
| 70 | +support vectors), so it is also memory efficient. |
| 71 | + |
| 72 | +Versatile: different Kernel functions can be specified for the decision |
| 73 | +function. Common kernels are provided, but it is also possible to |
| 74 | +specify custom kernels. |
| 75 | + |
| 76 | +*The disadvantages of support vector machines include:* |
| 77 | + |
| 78 | +If the number of features is much greater than the number of samples, |
| 79 | +avoid over-fitting in choosing Kernel functions and regularization term |
| 80 | +is crucial. |
| 81 | + |
| 82 | +SVMs do not directly provide probability estimates, these are calculated |
| 83 | +using an expensive five-fold cross-validation (see Scores and |
| 84 | +probabilities, below). |
| 85 | + |
| 86 | +The support vector machines in scikit-learn support both dense |
| 87 | +(numpy.ndarray and convertible to that by numpy.asarray) and sparse (any |
| 88 | +scipy.sparse) sample vectors as input. However, to use an SVM to make |
| 89 | +predictions for sparse data, it must have been fit on such data. For |
| 90 | +optimal performance, use C-ordered numpy.ndarray (dense) or |
| 91 | +scipy.sparse.csr_matrix (sparse) with dtype=float64 |
| 92 | + |
| 93 | +**Linear Kernel:** |
| 94 | + |
| 95 | +Function: 𝐾 ( 𝑥 , 𝑦 ) = 𝑥 𝑇 𝑦 |
| 96 | + |
| 97 | +Parameters: No additional parameters. |
| 98 | + |
| 99 | +**Polynomial Kernel:** |
| 100 | + |
| 101 | +Function: 𝐾 ( 𝑥 , 𝑦 ) = ( 𝛾 𝑥 𝑇 𝑦 𝑟 ) 𝑑 |
| 102 | + |
| 103 | +Parameters: |
| 104 | + |
| 105 | +γ (gamma): Coefficient for the polynomial term. Higher values increase |
| 106 | +the influence of high-degree polynomials. |
| 107 | + |
| 108 | +r: Coefficient for the constant term. |
| 109 | + |
| 110 | +d: Degree of the polynomial. |
| 111 | + |
| 112 | +**Radial Basis Function (RBF) Kernel:** |
| 113 | + |
| 114 | +Function: 𝐾 ( 𝑥 , 𝑦 ) = exp ( − 𝛾 ∣ ∣ 𝑥 − 𝑦 ∣ ∣ 2 ) |
| 115 | + |
| 116 | +Parameters: 𝛾 γ (gamma): Controls the influence of each training |
| 117 | +example. Higher values result in a more complex decision boundary. |
| 118 | + |
| 119 | +**Sigmoid Kernel:** |
| 120 | + |
| 121 | +Function: 𝐾 ( 𝑥 , 𝑦 ) = tanh ( 𝛾 𝑥 𝑇 𝑦 𝑟 ) |
| 122 | + |
| 123 | +Parameters: |
| 124 | + |
| 125 | +γ (gamma): Coefficient for the sigmoid term. |
| 126 | + |
| 127 | +r: Coefficient for the constant term. |
| 128 | + |
| 129 | + |
| 130 | +``` python |
| 131 | +import numpy as np |
| 132 | +import matplotlib.pyplot as plt |
| 133 | +from sklearn import svm, datasets |
| 134 | + |
| 135 | +# Load example dataset (Iris dataset) |
| 136 | +iris = datasets.load_iris() |
| 137 | +X = iris.data[:, :2] # We only take the first two features |
| 138 | +y = iris.target |
| 139 | + |
| 140 | +# Define the SVM model with RBF kernel |
| 141 | +C = 1.0 # Regularization parameter |
| 142 | +gamma = 0.7 # Kernel coefficient |
| 143 | +svm_model = svm.SVC(kernel='rbf', C=C, gamma=gamma) |
| 144 | + |
| 145 | +# Train the SVM model |
| 146 | +svm_model.fit(X, y) |
| 147 | + |
| 148 | +# Plot the decision boundary |
| 149 | +x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1 |
| 150 | +y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1 |
| 151 | +xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02), |
| 152 | + np.arange(y_min, y_max, 0.02)) |
| 153 | +Z = svm_model.predict(np.c_[xx.ravel(), yy.ravel()]) |
| 154 | +Z = Z.reshape(xx.shape) |
| 155 | + |
| 156 | +plt.contourf(xx, yy, Z, cmap=plt.cm.Paired, alpha=0.8) |
| 157 | + |
| 158 | +# Plot the training points |
| 159 | +plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired) |
| 160 | +plt.xlabel('Sepal length') |
| 161 | +plt.ylabel('Sepal width') |
| 162 | +plt.title('SVM with RBF Kernel') |
| 163 | +plt.show() |
| 164 | +``` |
| 165 | + |
| 166 | + |
| 167 | +- Data Preprocessing |
| 168 | + Data preprocessing is a crucial step in the machine learning pipeline |
| 169 | +that involves transforming raw data into a format suitable for training |
| 170 | +a model. Here are some fundamental techniques in data preprocessing |
| 171 | +using scikit-learn: |
| 172 | + |
| 173 | +**Handling Missing Values:** |
| 174 | + |
| 175 | +Imputation: Replace missing values with a calculated value (e.g., mean, |
| 176 | +median, mode) using SimpleImputer. Removal: Remove rows or columns with |
| 177 | +missing values using dropna. |
| 178 | + |
| 179 | +**Feature Scaling:** |
| 180 | + |
| 181 | +Standardization: Scale features to have a mean of 0 and a standard |
| 182 | +deviation of 1 using StandardScaler. |
| 183 | + |
| 184 | +Normalization: Scale features to a range between 0 and 1 using |
| 185 | +MinMaxScaler. Encoding Categorical Variables: |
| 186 | + |
| 187 | +One-Hot Encoding: Convert categorical variables into binary vectors |
| 188 | +using OneHotEncoder. |
| 189 | + |
| 190 | +Label Encoding: Encode categorical variables as integers using |
| 191 | +LabelEncoder. |
| 192 | + |
| 193 | +**Feature Transformation:** |
| 194 | + |
| 195 | +Polynomial Features: Generate polynomial features up to a specified |
| 196 | +degree using PolynomialFeatures. |
| 197 | + |
| 198 | +Log Transformation: Transform features using the natural logarithm to |
| 199 | +handle skewed distributions. |
| 200 | + |
| 201 | +**Handling Outliers:** |
| 202 | + |
| 203 | +Detection: Identify outliers using statistical methods or domain |
| 204 | +knowledge. Transformation: Apply transformations (e.g., winsorization) |
| 205 | +or remove outliers based on a threshold. |
| 206 | + |
| 207 | +**Handling Imbalanced Data:** |
| 208 | + |
| 209 | +Resampling: Over-sample minority class or under-sample majority class to |
| 210 | +balance the dataset using techniques like RandomOverSampler or |
| 211 | +RandomUnderSampler. |
| 212 | + |
| 213 | +Synthetic Sampling: Generate synthetic samples for the minority class |
| 214 | +using algorithms like Synthetic Minority Over-sampling Technique |
| 215 | +(SMOTE). Feature Selection: |
| 216 | + |
| 217 | +Univariate Feature Selection: Select features based on statistical tests |
| 218 | +like ANOVA using SelectKBest or SelectPercentile. |
| 219 | + |
| 220 | +Recursive Feature Elimination: Select features recursively by |
| 221 | +considering smaller and smaller sets of features using RFECV. |
| 222 | + |
| 223 | +**Splitting Data:** |
| 224 | + |
| 225 | +Train-Test Split: Split the dataset into training and testing sets using |
| 226 | +train_test_split. |
| 227 | + |
| 228 | +Cross-Validation: Split the dataset into multiple folds for |
| 229 | +cross-validation using KFold or StratifiedKFold. |
0 commit comments